2018S.1.3
Po pierwsze - jak poprawić mój zapis?
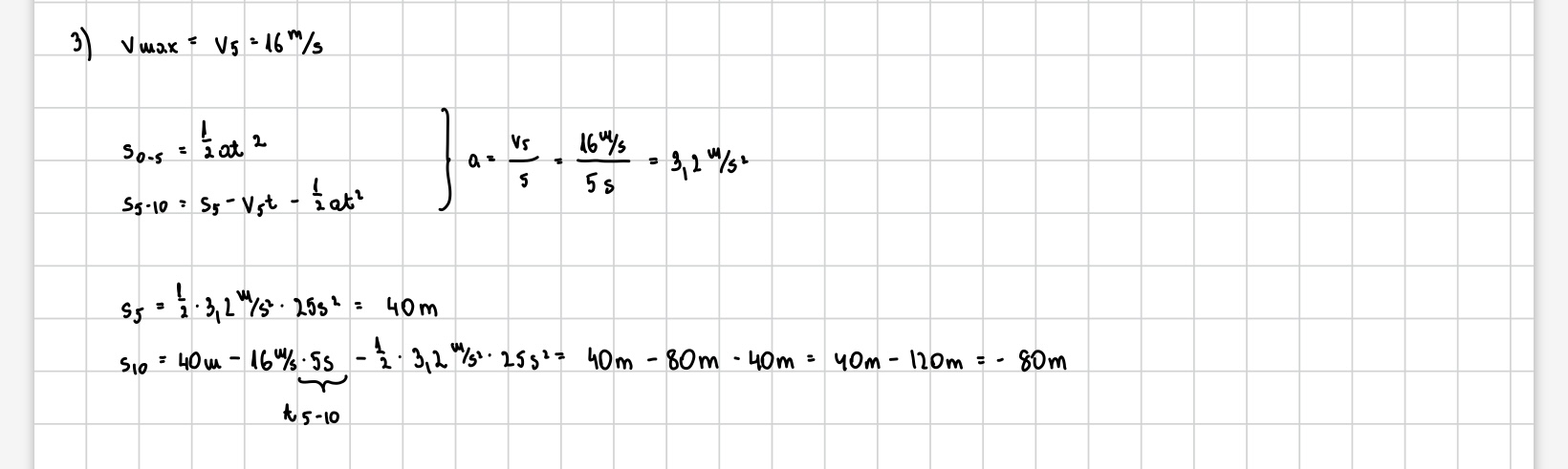
Jak wyznaczyłam drogę przebytą do 5s to wyszło poprawnie. Natomiast, gdy policzyłam drogę przebytą od 5s do 10s, kiedy ruch był jednostajnie opóźniony, więc skorzystałam z równania na ruch opóźniony, droga w 10s wyszła mi ujemna (ale patrząc na odpowiedź CKE sam wynik 80m już jest dobry).
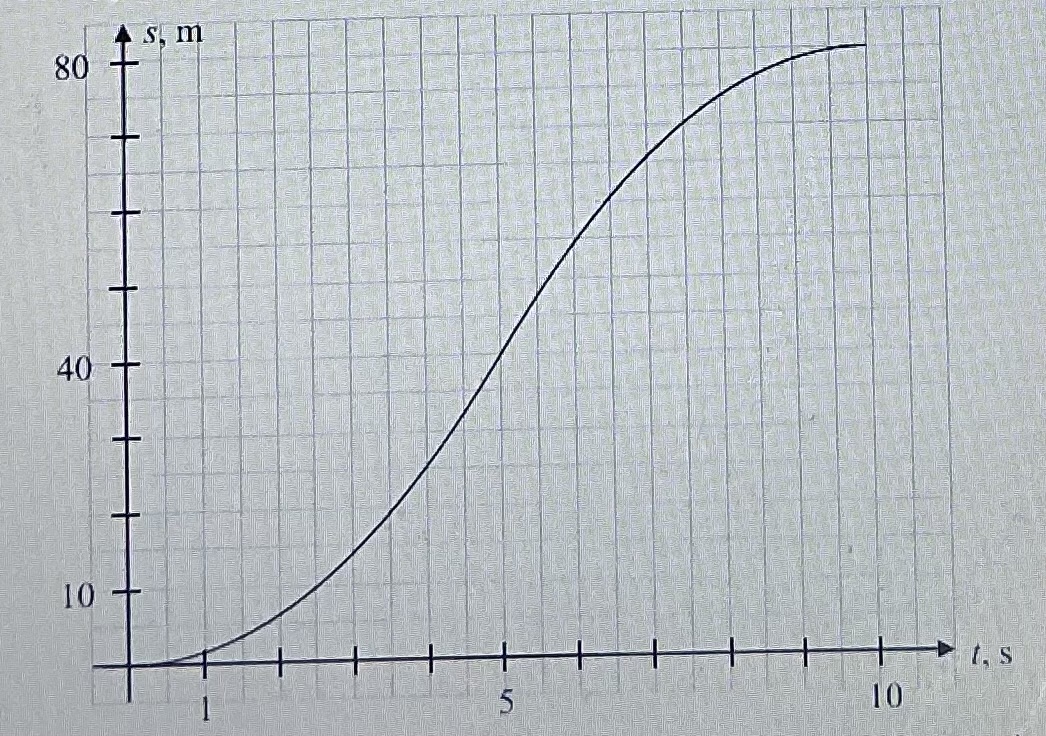
i druga część pytania - dlaczego ten wykres będzie miał taki kształt? Dlaczego nie jest on prostą linią?
Fizyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przed członem gdzie przemnażasz v0*t powinien stać plus i wtedy dostaniesz 40 m + 80 m - 40 m = 80 m. Musi tak być ponieważ, gdy ruch jest jednostajnie opóźniony, to wyrażenia z prędkością początkową i przyspieszeniem muszą być przeciwnych znaków. Stąd przed członem v0*t znak musi być dodatni, a potem przed członem z przyspieszeniem (opóźnieniem) znak musi być ujemny.
Co do kształtu wykresu - wynika to z faktu jaka jest zalezność przebytej drogi od czasu w ruchu jednostajnie zmiennym. Jak sama zapisałaś w obliczeniach s(t) jest przecież funkcją kwadratową (np. w ruchu przyspieszonym mamy s = v0*t + 1/2 * a * t^2), w związku z tym wykresem musi być fragment paraboli. Tutaj jest to tak naprawdę połączenie dwóch ruchów jednostajnie zmiennych. Od 0 do 5 s jest to ruch przyspieszony (znak przed członem 1/2 * a * t^2 jest dodatni, stąd kształt paraboli jest taki, że jej ramiona - tu mamy jedno jej ramię - są zwrócone w górę). Od 5 s do 10 s ruch jest opóźniony (znak przed członem 1/2 * a * t^2 jest ujemny, więc jest to fragment paraboli z ramionami zwróconymi w dół).
Wykres byłby liniowy w przypadku ruchu jednostajnego (tam bowiem s = v*t i jest to faktycznie funkcja liniowa).