Domowe 10 cz1 1A

Mam pytanie - czy w tym zadaniu nie powinno się również rozpatrzyć przypadku zerowego? W kryteriach go nie ma i też np. w podobnym zadaniu CKE, gdy robi się je metodą funkcji kwadratowej CKE nie wymaga przypadku zerowego (2017 maj zadanie 7). Dlaczego w tego typu zadaniach w kryteriach nie ma przypadku zerowego? Czy zapisanie przypadku zerowego powoduje obniżkę punktacji?
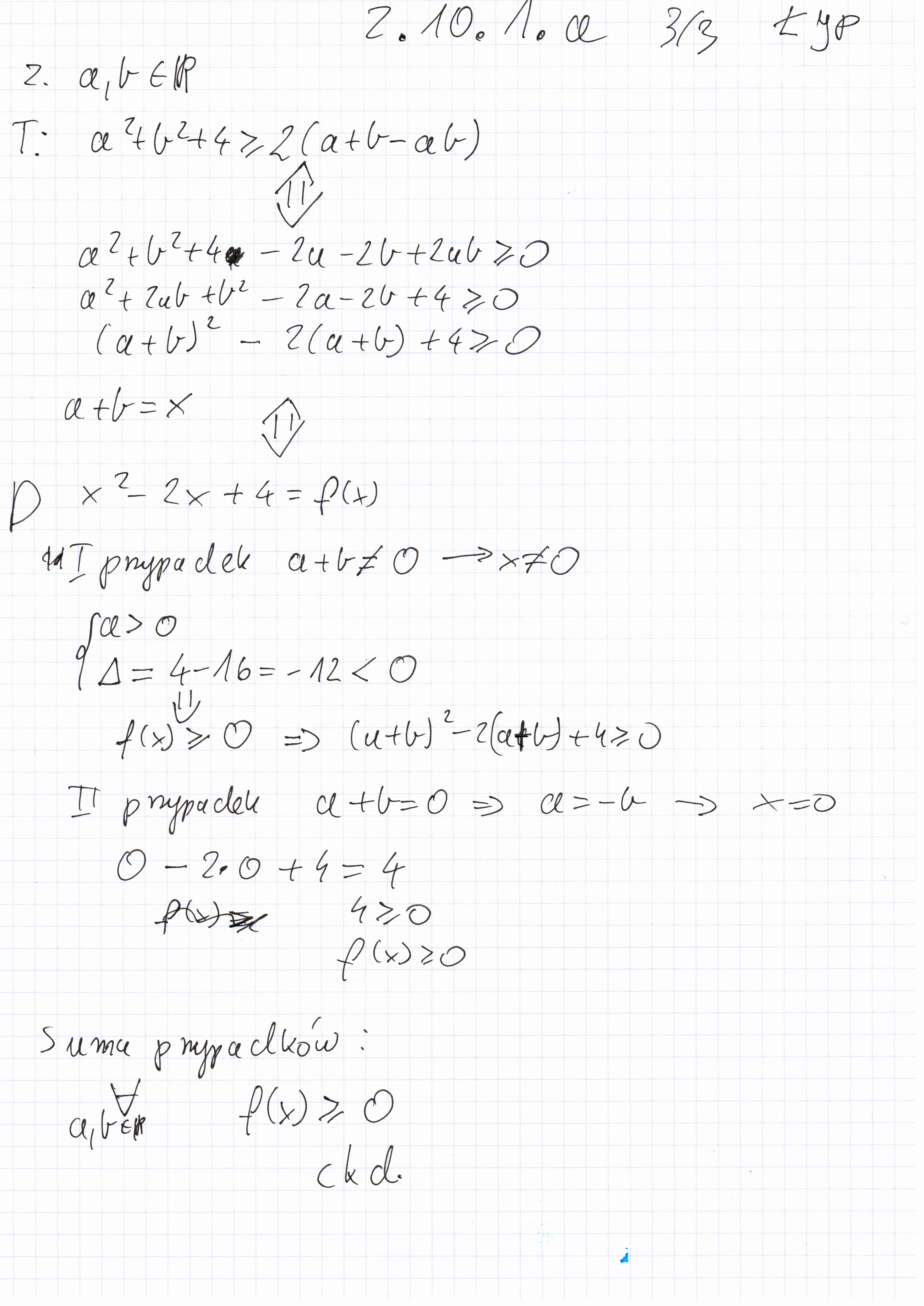
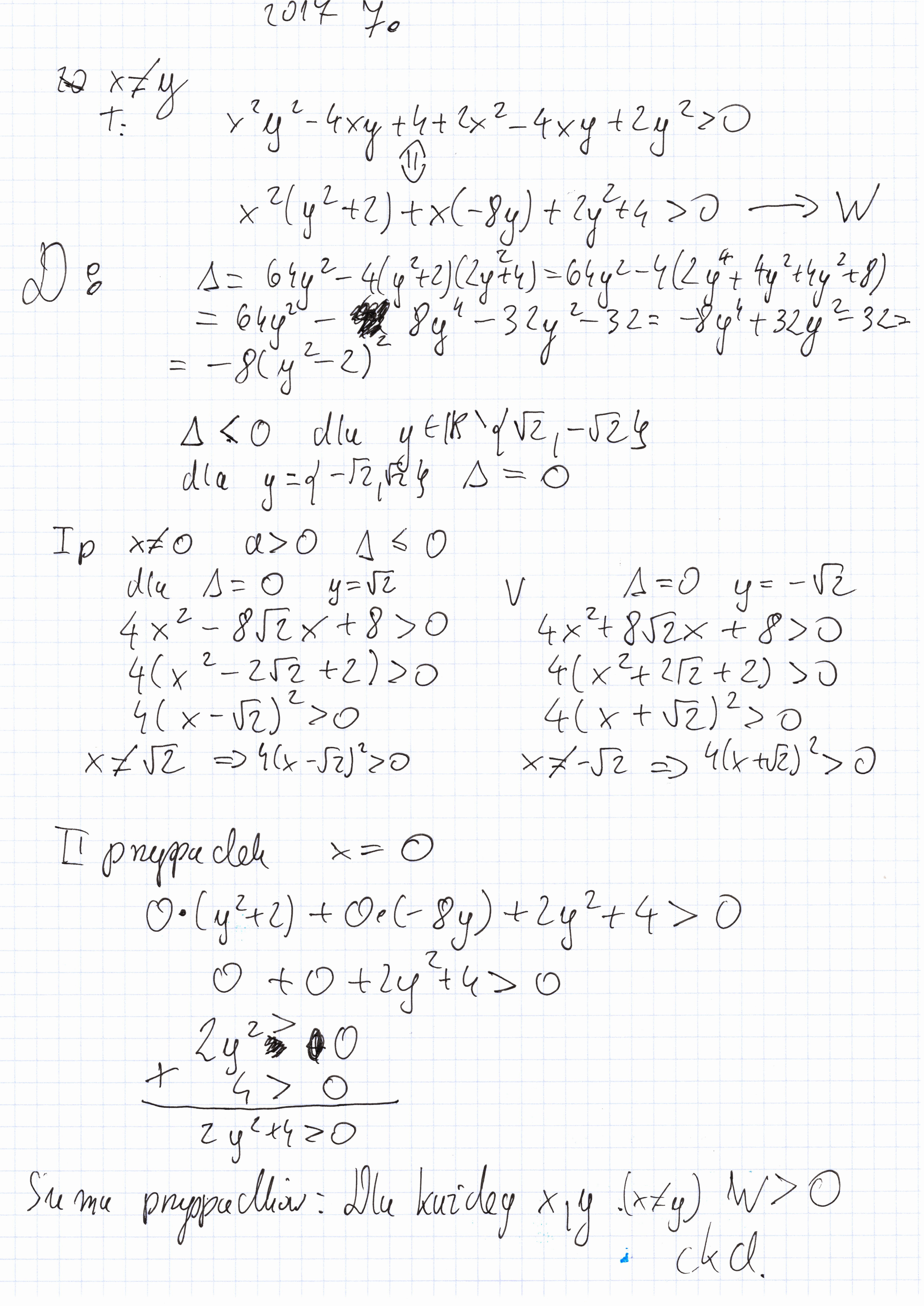
Dowodzenie nierówności matematyka rozszerzona Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Delta równa zero to nie przypadek zerowy, przypadek zerowy/liniowy to sytuacja, gdy całkowicie kasuje się wyraz a w funkcji kwadratowej, a ponieważ tu mamy jeszcze zerowanie wyrazu b to zostaje funkcja stała. To są inne sytuacje - delta masz zero gdy y=pierw2 lub y=-pierw2
A przypadek zerowy, gdy zeruje się x, albo całe a+b
Analogicznie w równaniu kwadratowym z parametrem. Robisz dwa przypadki, gdy jest funkcja kwadratowa i drugi gdy jest funkcja liniowa, czy szczególny jej przypadek liniowa stała jaka i w obu tych zadaniach wychodzi
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przypadek zerowy funkcji kwadratowej odnosi się do sytuacji, w której funkcja kwadratowa ma brak miejsc zerowych, czyli nie przecina osi OX
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To jasne i to rozpatrzyłem - wychodzi funkcja stała spełniająca nierówność zarówno w pierwszym jak i drugim zadaniu. Pytanie dlaczego rozpatrzenie tego przypadku nie jest wymagane ani przez zbiór zadań z kursu ani przez CKE w 2017 r.
jak robimy funkcje kwadratowe takie przypadki rozpatrujemy
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Widzę że ucieło mi połowe wypowiedzi na poprzednim wpisie - Bo rozwiązanie nic nie wniesie i cke po prostu go nie zapisało. Gdyby coś zmieniało to na pewno by zapisali.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tu pełna zgoda, zresztą nie może nic wnosić, bo musi potwierdzić dowód (gdyby wniósł coś innego to by go obalił), tylko dalej nie jestem przekonany dlaczego - w sensie w nierównościach kwadratowych też liczymy te nic nie wnoszące przypadki, czasem jeden zawiera się w drugim a i tak ucinają punkty za nierozpatrzenie każdego możliwego przypadku.
Tu w wypadku zadania 2017.7 rozpatrujemy y w R i x w R-{0}. Rozpatrzenie x=0 to tak naprawdę w jednej linijce można zrobić i mamy pewność.
To samo w zadaniu z kursu, nie mamy rozpatrzonego przypadku, gdy a i b = 0 (nie ma napisane, że są różne) ani przypadku, gdy są są sobie przeciwne.
No i dalej aktualne pozostaje pytanie - czy obetną punkty za rozpisanie dla pewności tej sytuacji
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No taką mam nadzieję, ale cóż - w tym zadaniu w stosunku do innych nie widzę konsekwencji, bo zawsze każdy możliwy przypadek trzeba rozpatrzeć.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Na marginesie dyskusji wrzucę przypadek, gdy CKE wymaga, rozpatrzenia tego co się dzieje jak się zeruje niewiadoma
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
MarcinC
Co rozumiesz poprzez "rozpatrzenie przypadku zerowego"?
Jeżeli mamy udowodnić, że jakieś wyrażnie "A" jest większe lub równe od zera. I uda nam się wykazać, że wyrażenie A jest większe od zera to dowód jest zakończony.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wciąż czegoś nie rozumiem. Rozumiem, że w przytoczonych przypadkach współczynnik kierunkowy jest znany i nierówny 1, więc nie ma sensu rozważać przypadku liniowego, ale mając do udowodnienia pewną nierówność kwadratową ax² + bx + c > 0, której współczynnika kierunkowego nie znamy, MUSIMY się chyba upewnić, że funkcja jest ZAWSZE dodatnia, również w przypadku liniowym kiedy a się zeruje, prawda? Miałem taką sytuacje w podpunkcie k kiedy próbowałem go rozwiązać tym sposobem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Oczywiście, jeżeli mamy: ax² + bx + c > 0,
I musimy udowodnić, że ta funkcja dla x e R jest zawsze > 0 to musimy wykazać, że a>0 oraz delta < 0
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
ale jeśli w tym przypadku nie znałem współczynnika kierunkowego (który paradoksalnie wynosi tutaj b) to czy dobrze zrobiłem, że uwzględniłem przypadek liniowy? Oczywiście zaraz go odrzuciłem, bo założenia wykluczały taką możliwość, ale co gdyby nie wykluczały? No bo gdyby teoretycznie współczynnik kierunkowy wynoszący b mógłby być zerem, to czy w takiej sytuacji nie dochodzi nam dodatkowe rozwiązanie, czyli funkcja stała nad osią x? (też spełnia wymaganie f(x) > 0, ale samym przypadkiem a > 0 i delta < 0 tego rozwiązania nie wyłapiemy, bo współczynnik kierunkowy jest tutaj równy zero.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie ma problemu z tym, że pierw rozpisałeś warunki do przypadku liniowego, a później go odrzuciłeś. Gdyby b należało do liczb rzeczywistych należałoby rozważyć dodatkowe przypadki.
I tak jeżeli wsp. przy "a^2" oraz "a" byłby 0 to zostaje nam samo b.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale oni rozpatrzyli przypadek zerowy. Wszystko co jest pod deltą to jest rozpatrzenie delta=0