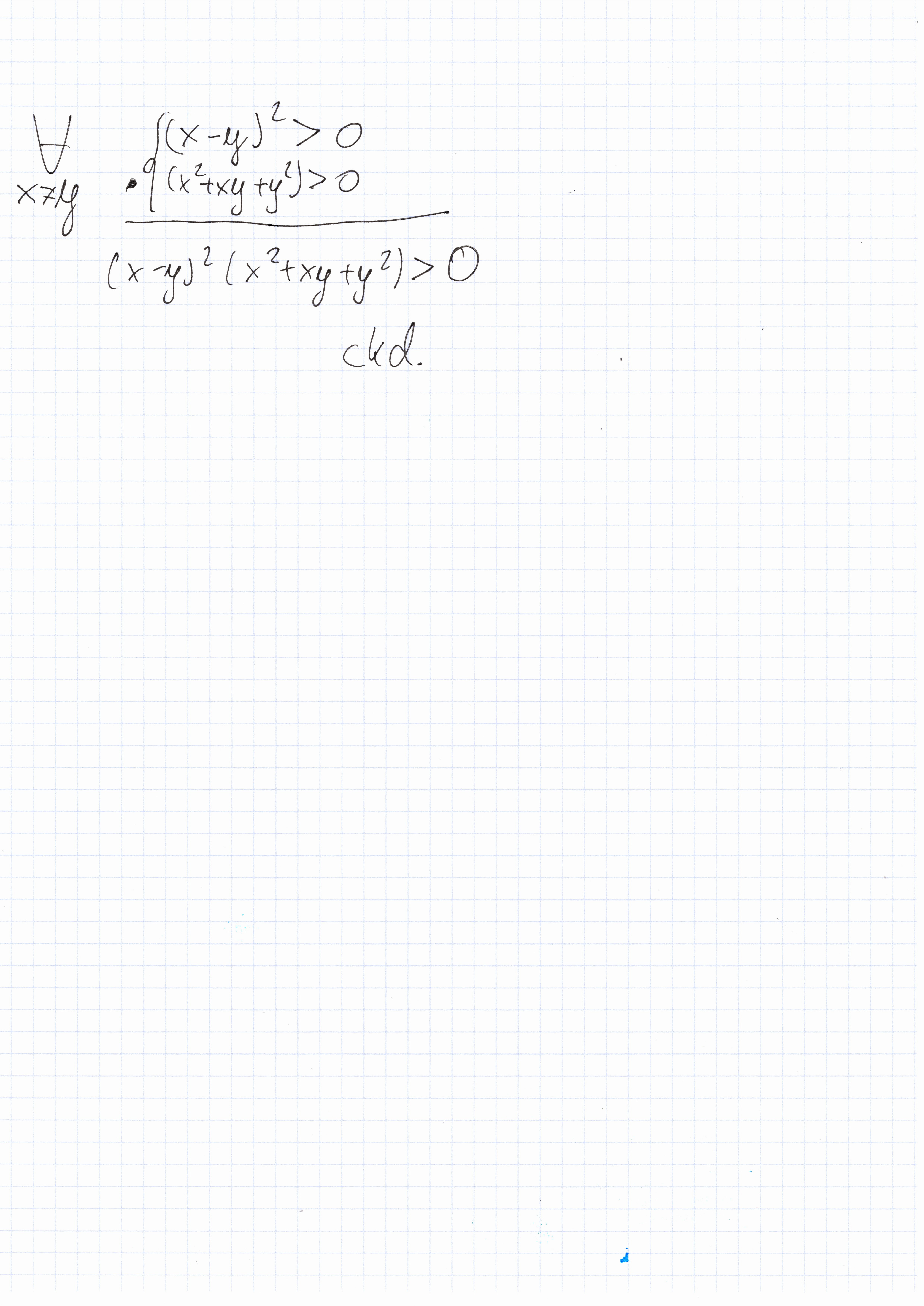2022.C.6
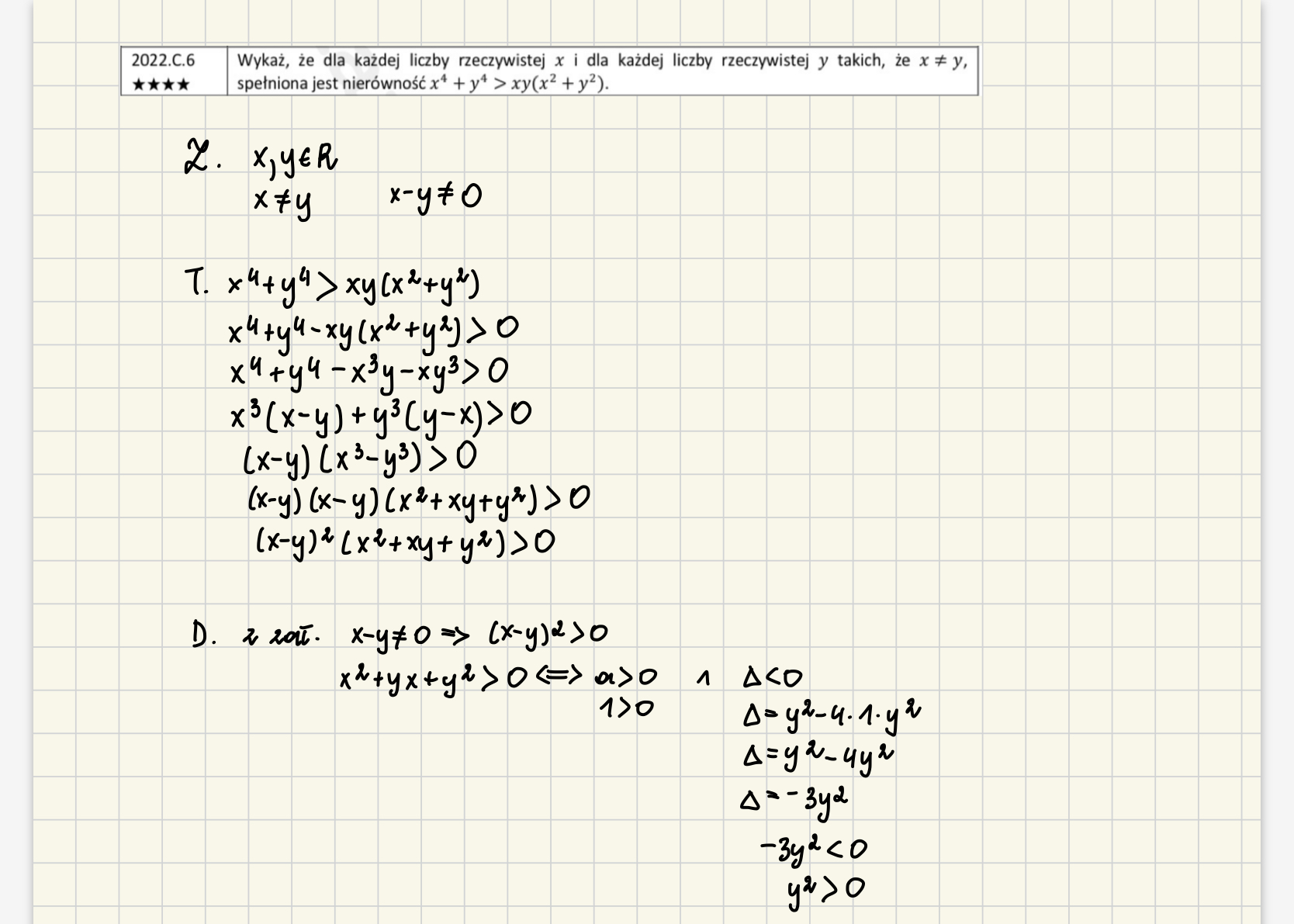
nie wiem jak dokończyć ten dowód
dowodzenie nierówności Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
ale tutaj chyba y może się równać 0 i wtedy y*2>0 nie jest poprawne i nie wiem czy to trzeba rozbić na jakieś dwa przypadki czy jak
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak - umknął mi ten przypadek zerowy, bo raz go wymagają a raz nie. Trzeba zapisać, ze gdy x=0 to y^2>0 lub gdy y=0 to x^2>0

- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Co do rozpatrywania tego zera to zerknij sobie dyskusje w moim temacie:
Domowe 10 cz1 1A - Szkoła Maturzystów
Ja jutro poproszę, może Pana Łukasza Jarosińskiego, żeby zerknął jak to jest z tym zerowaniem, więc możesz zerknąć temat
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. czyli ten przypadek z 0 trzeba uwzględniać (jeśli w ogóle) w sytuacjach, gdzie dowodzimy z wykorzystaniem funkcji kwadratowej? bo w zadaniu 2017.7, które poruszałeś w tej dyskusji jeśli się je zrobi metodą dopełnienia do kwadratów (tak jak my na lekcji) to wtedy chyba tego przypadku nie ma po co rozpatrywać
2. czy teraz to rozwiązanie jest w pełni poprawne i punktowane? i czy muszę zapisywać te dwa równania w klamrze z mnożeniem czy tak jak zapisałam wystarczy?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak jak na zajęciach - mnożymy stronami i otrzymujemy przekształconą tezę