2019.C.9

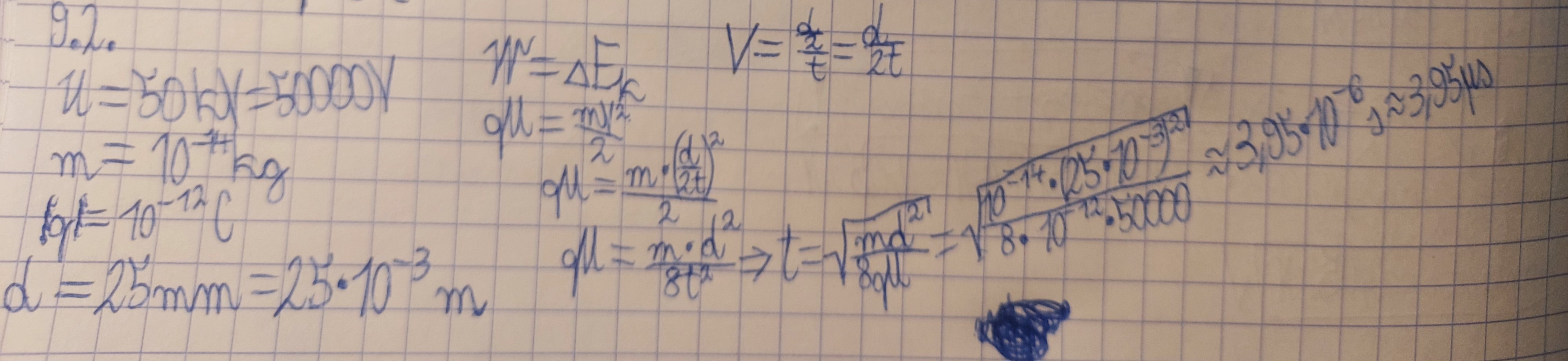
Dlaczego takie rozwiązanie nie jest poprawne?
Fizyka elektrostatyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A przyjmujemy, że V0=0?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

To i tak dalej mi nie wychodzi :(
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ok, teraz zapis z prędkością jest ok. Natomiast masz tam jeszcze drobny błąd z wrzucanym napięciem (przepraszam, że wcześniej tego nie zauważyłem, ale od razu w oczy rzuciła mi się ta prędkość i pominąłem to napięcie). Chodzi o to, że w tym wzorze wrzucamy napięcie między punktami, między którymi przemieściło się ciało. W naszym przypadku drobina nie przemieściła się pomiędzy płytkami, tylko pomiędzy środkiem kondensatora a jedną płytką. Nie pokonała zatem różnicy napięć równej 50 kV, ale połowę tej wartości - trzeba zatem tam włożyć 25 kV i wtedy wyjdzie dobrze.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Aha czyli to tak działa. Czyli jaką część odległości między płytami pokona drobina takie napięcie jakby pokona?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak. Wynika to wprost ze wzoru, który jest w karcie: U = E*d. Możemy sobie bowiem wyobrazić np. kondensator, w którym natężenie jest takie samo, ale odległości między okładkami są np. dwukrotnie bliżej siebie. To oznacza, że napięcie między nimi będzie dwukrotnie mniejsze. I do tego wzoru w ogólności można wrzucać różne odległości d, dzięki czemu będziemy uzyskiwać proporcjonalne wartości "przebytego" napięcia.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A jakby natężenie pola elektrycznego się zmieniało? To wtedy już chyba tak nie zadziała.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A w sposobie podawanym przez cke wychodzi na to, że nie trzeba wiedzieć, że napięcie jest równe U/2.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No bo to jest inny sposób, w którym wykorzystujesz obliczenie przyspieszenia, a w nim wykorzystujesz wartość natężenia pola elektrycznego, a to natężenie E można obliczyć jako E = U/d. Zauważ natomiast, że wynik oczywiście ostatecznie jest taki sam.
Co do wcześniejszego pytania, to gdyby pole się zmieniało, to oczywiście nie można byłoby tego w ten sposób liczyć (ani jednym, ani drugim sposobem), bo wtedy już nie mielibyśmy pola jednorodnego...
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A rzeczywiście nigdy wcześniej o tym nie myślałem, że jak pole jest jednorodne to E=const., a jednak sama nazwa wskazuje na to. Dziękuję :D
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No dokładnie, nazwa tu wiele mówi ;) nie ma sprawy :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bo prędkość jaką osiąga drobina w momencie uderzenia w płytkę nie jest równa d/2t. Tak by było, gdyby jej ruchem był ruchem jednostajnym (dzielimy wtedy faktycznie po prostu drogę przez czas), ale tu ruch drobiny nie jest oczywiście ruchem jednostajnym.