2016.C.11
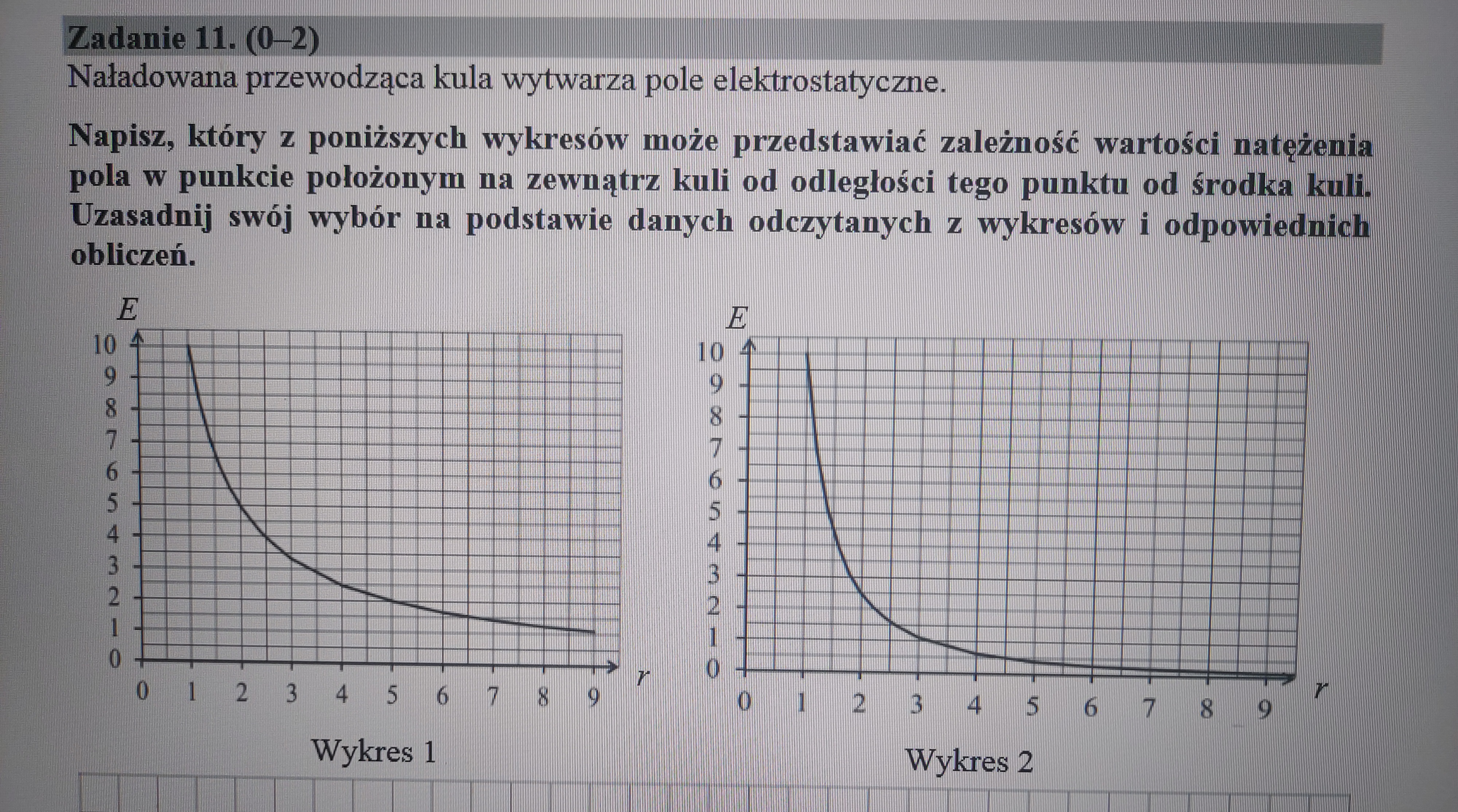
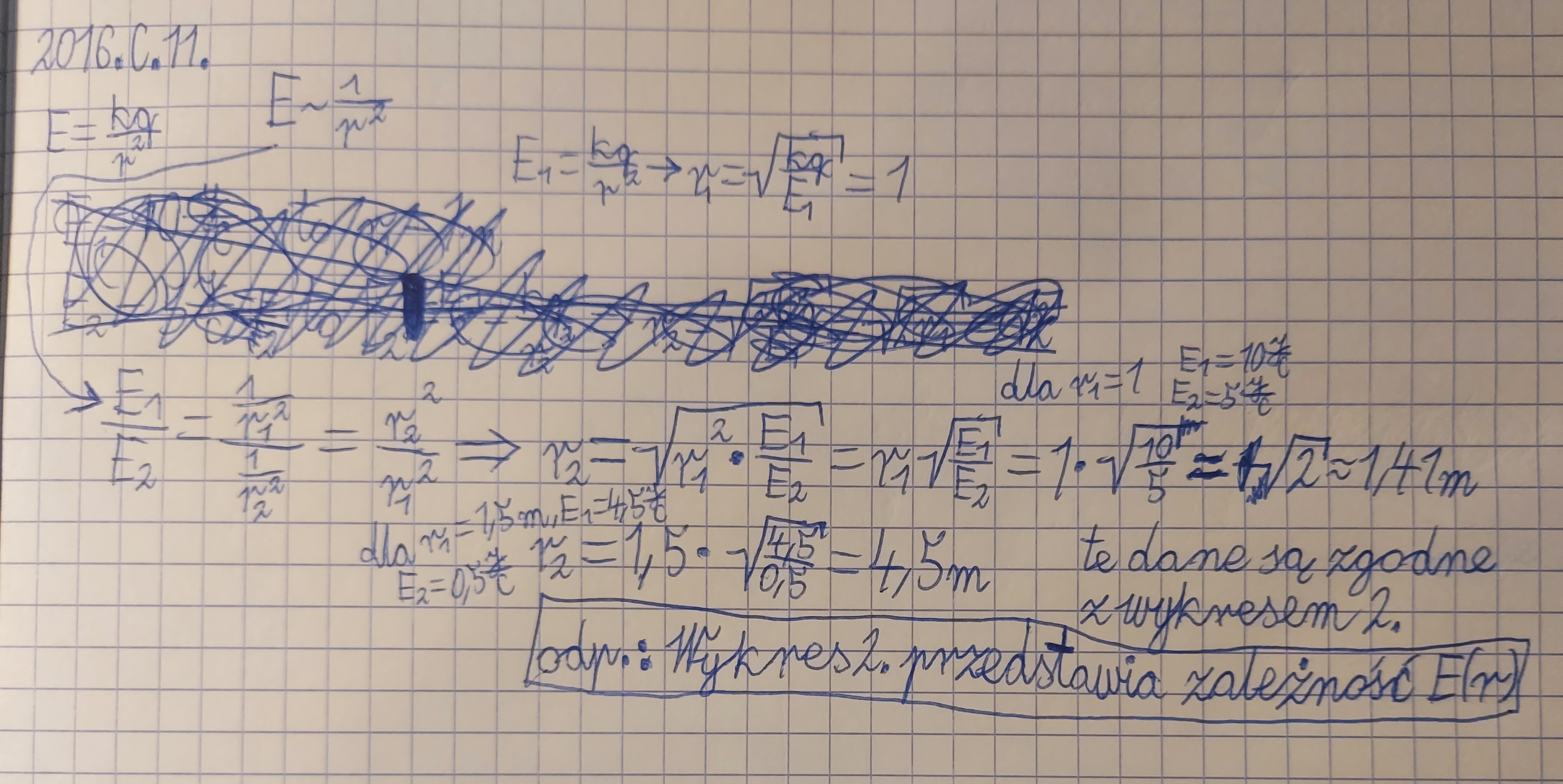
Czy takie uzasadnienie wystarczy? I czy można to uzasadnić z granic? Czyli dla "r" dążącego do nieskończoności "E" dąży do 0.
Fizyka elektrostatyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli nadmiernie skomplikowałem ale jest ok. A jeśli w treści nie podali jednostek to też mogę liczyć tylko na liczbach?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No cóż, teoretycznie nie wiesz jakie tam są jednostki, więc sam sobie tutaj coś zakładasz, natomiast nie zmienia to samego procesu wnioskowania, więc myślę, że zostałoby to uznane :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, to jest ok, choć według mnie nawet nadmiernie to skomplikowałeś ;) wystarczyłoby np. zauważyć, że dla r = 1 w obu przypadkach E = 10. Aby wykres był poprawny to z zależności wartości natężenia od odległości od środka kuli wynika, że wartość E dla r = 2 musi być czterokrotnie mniejsza, czyli E = 2,5. No i widzimy, że faktycznie drugi wykres spełnia ten warunek, a pierwszy nie.
Swoją drogą to wielkości podane na wykresach nie mają konkretnych jednostek, więc używanie metrów dla r nie jest do końca zgodne z danymi, ale pewnie by to przeszło. A druga rzecz, to taka, że J/C w ogóle nie jest jednostką E - jego jednostką jest N/C.
Co do pytania o granice to tutaj niczego by to nie rozstrzygnęło - nie wiemy bowiem do jakiej wartości dążą E na przedstawionych wykresach. Tzn. możemy zauważyć, że najprawdopodobniej na wykresie nr 2 faktycznie dąży to do 0, ale zgodnie z wykresem nr 1 też ciągle ta wartość maleje, więc tam ona również "być może" dąży do zera (i w istocie tak by było, bo na pierwszym wykresie przedstawiona jest zależność 1/r). Więc żadnej informacji w kwestii rozstrzygnięcia tego, który wykres jest poprawny by nam to nie przyniosło.