Kurczab zad.2.181
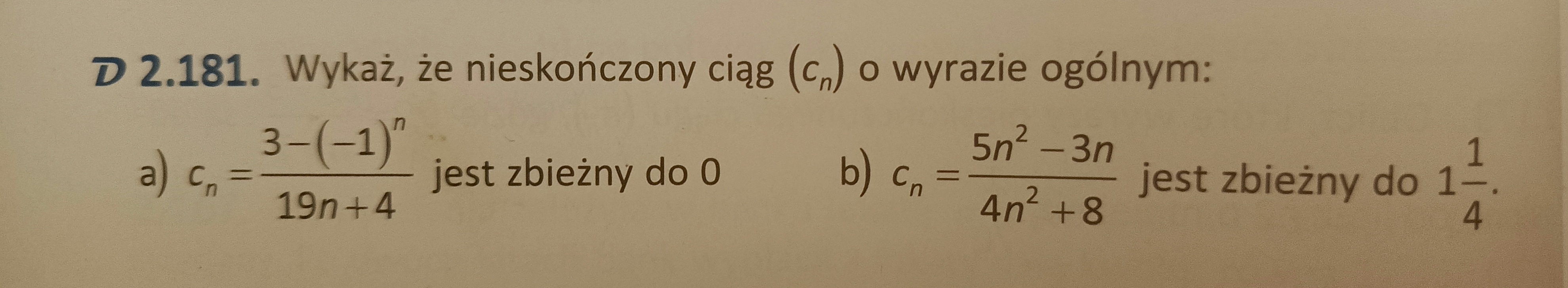
Prosiłabym o wytłumaczenie tego zadania i ogólnie jak powinno się przeprowadzać dowody z definicji, że dana liczba jest/nie jest granicą ciągu.
Matematyka rozszerzona Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dziękuję:) Mam jeszcze jednak pytanie do podpunktu b, bo chciałam tak przeprowadzić dowód, ale nie wiem co powinnam zrobić dalej w takim przypadku?

- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Należy teraz wyznaczyć "n" w zależności od wartości epsilon.
A następnie dobrać takie N, żeby dla każdego n>N, nierówność była spełniona.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Proszę Pana, a czy takie dokończenie zadania jest poprawne? I czy można napisać między tezą a nierównością |cn - 1 ¼|<ε znak równoważności na początku zadania?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie można w ten sposób podstawić n^3 podczas przekształcenia ponieważ jest to nieodwracalne przekształcenie.
Jezeli chodzi o znak rownowaznosci to można, ale trzeba dopisac kwantyfikatory z definicji granicy
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W takim razie jak powinnam przekształcić tę nierówność, żeby otrzymać n po jednej stronie? Próbowałam na różne sposoby, ale niestety nie udaje mi się i proszę o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dziękuję Panu bardzo:) Mam tylko kilka pytań:
Skąd jest 1 w N=n1 + 1?
Dlaczego n2=3+√169-128ε nie dzieli się na 8ε tak jak n1?
Dlaczego końcowo n ∈ (N,+∞) ∩ (n2, +∞)?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1)
Tam jest N= n2+1 (to +1 można pominąć, jest tylko po to aby ewentualnie powiększyć N jeśli pasują nam trochę większe)
2) Powinno się dzielić
3) Chodzi o to że biorąc każdy n większy N jest spełniona nierówność |c_n-5/4] < E bo wiemy że n należy do (N, +niesk) bo zawiera się w (n2; +niesk) co jest wynikiem naszego obliczonego wcześniej rozwiązania nierówności
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dziękuję, już rozumiem:)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Tutaj wystarczy obliczyć granicę:
na przykładzie podpunktu
b)
Jeżeli wyciągniemy n^2 przed nawias zarówno w liczniku i mianowniku możemy zauważyć, że -3n/n^2 będzie zbiegać do zera oraz 8/n^2 również. Pozostanie nam zatem 5/4 czyli 1 i 1/4.