INF 18.2
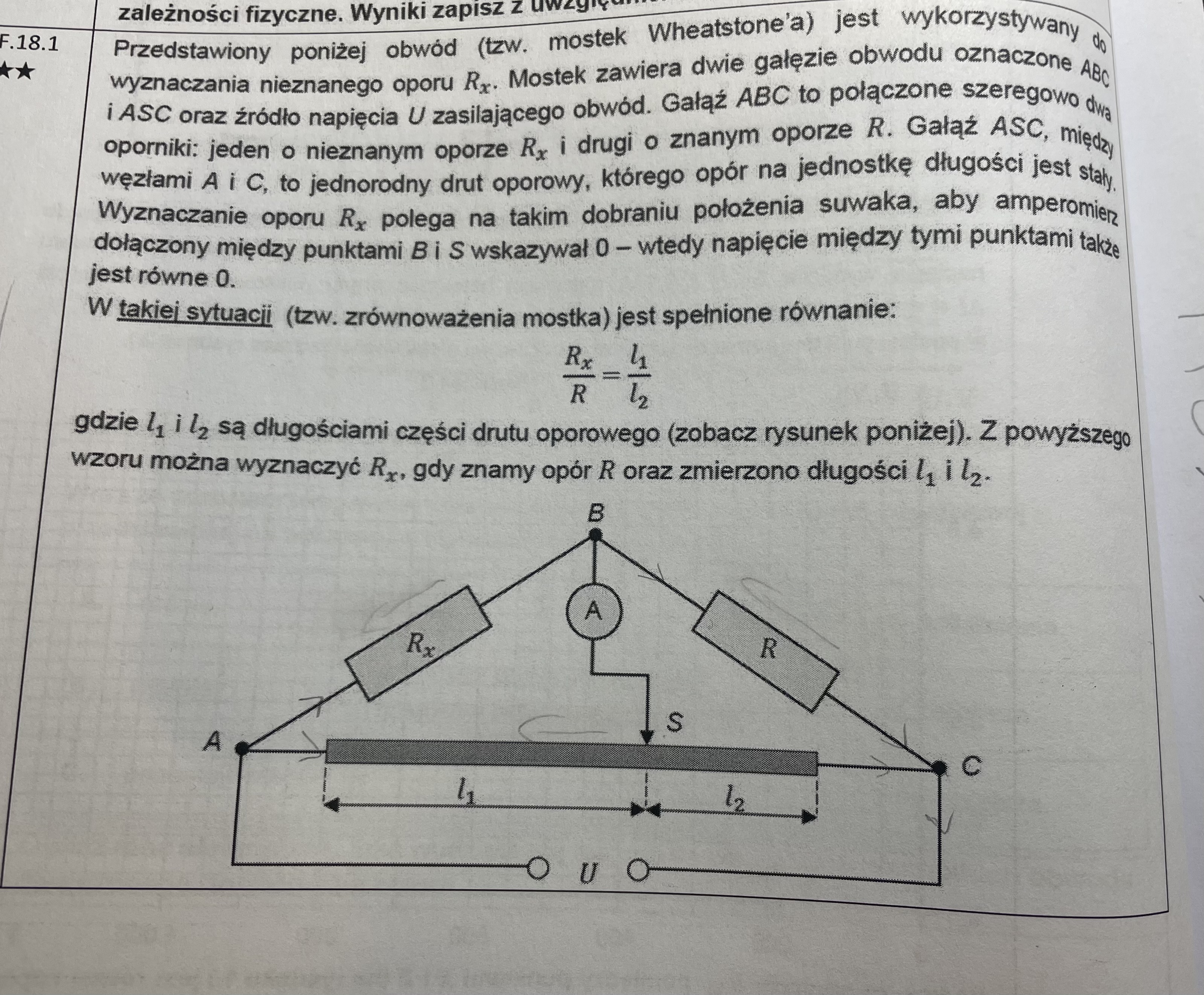

Jak wyprowadzić ten wzór?
Fizyka informator wyprowadzenie Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A mógłby pan na rysunku pokazać jeszcze dlaczego tak jest, że Uab=Uas?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Łatwiej niż pokazywać na rysunku jest to chyba wytłumaczyć ;) tzn. skoro mostek jest zrównoważony, to oznacza, że między punktami B i S nie płynie prąd. A to oznacza, że punkty B i S mają taki sam potencjał. A jeśli tak, to różnica potencjałów (czyli napięcie) między A i B jest taka sama jak między A i S.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A rzeczywiście. Ale ta różnica potencjałów (Ubs=0), bo z treści zadania wiemy, że Ibs=0 tak?
Czyli tak byłoby ok?

- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Odpowiedź na oba pytania brzmi tak :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Po pierwsze należy pamiętać, że zgodnie ze wzorem R = ro*l/S, opór drutu oporowego jest proporcjonalny do długości tego drutu. Czyli te fragmenty o długościach l1 i l2 możemy traktować w zasadzie jako takie oporniki o odpowiednio proporcjonalnych do swoich długości oporach (oznaczmy je jako Ras i Rsc).
No i teraz należałoby wykorzystać prawa Kirchhoffa. Z II prawa Kirchhoffa wynika np. fakt, że napięcia Uab = Uas oraz Ubc = Usc (bo pomiędzy B i S nie płynie prąd). Przyjmując teraz, oznaczenia takie że przez "górną część" obwodu (czyli przez oporniki Rx i R) płynie prąd Ib, a przez drut oporowy płynie prąd Is i wykorzystując prawo Ohma można zatem zapisać, że Ib*Rx = Is*Ras (wynika to z równania Uab = Uas), a z drugiego równania na napięcia dostajemy Ib*R = Is*Rsc. I z tych równań można już dojść do ostatecznego wzoru pamiętając, że Ras jest wprost proporcjonalne do l1, a Rsc jest wprost proporcjonalne do l2.