zad. 13 Nowa Era
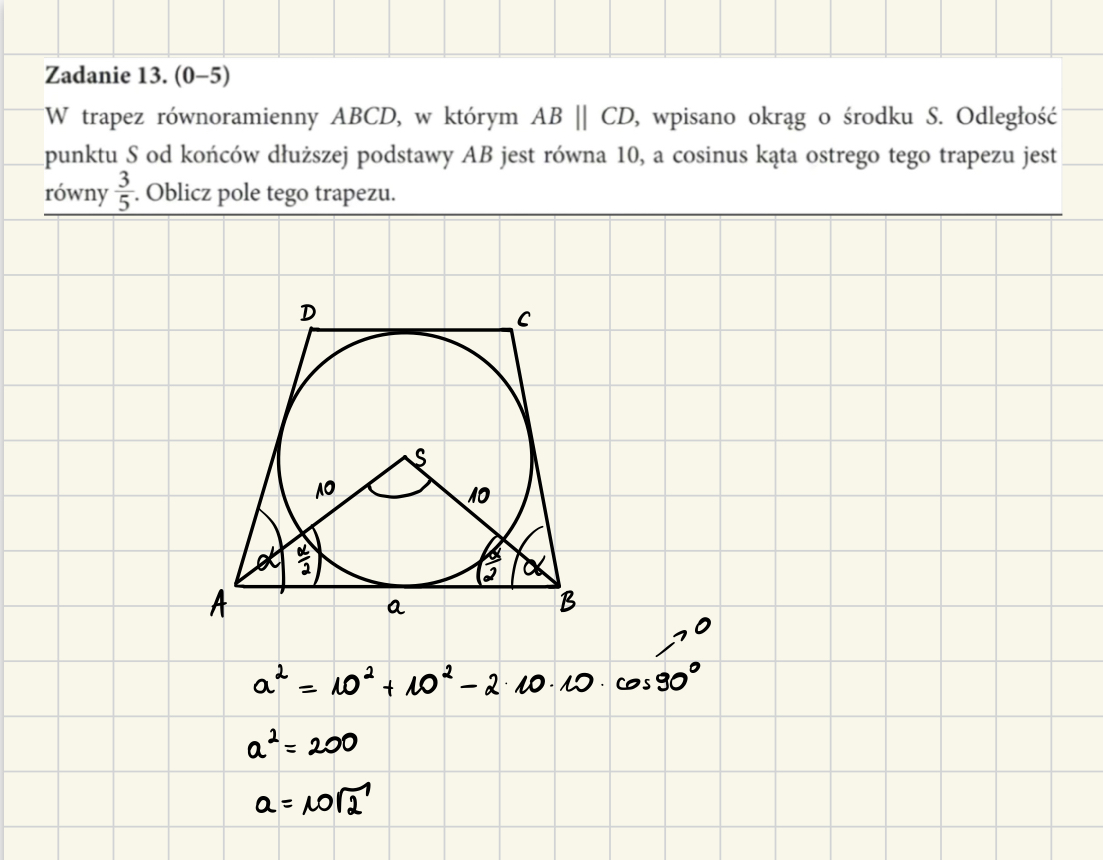
Według twierdzenia 10 z lekcji, które było omawiane przy zadaniu 60 ze zbioru zadań, dwusieczne w trapezie opisanym na okręgu przecinają się pod kątem prostym. Dlaczego to twierdzenie nie działa natomiast w tym zadaniu? Wtedy skoro AS i BS to dwusieczne to kąt ASB miałby 90 stopni i w twierdzeniu cosinusów uzyskalibyśmy, że bok a wynosi 10 pierwiastków z 2, a ma wynosić 8 pierwiastków z 5.
planimetria Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
założyłam tak, bo S to środek okręgu, a środek okręgu wpisanego to miejsce przecięcia się dwusiecznych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zgadza się - uzasadnij dlaczego teraz ASB miałby mieć 90 stopni.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Myślałam, że kąt ASB będzie miał 90 stopni, bo kierowałam się twierdzeniem 10. Ale rozumiem, że to twierdzenie jednak nie będzie tutaj działało, bo w jego dowodzie, trzeba wykorzystać fakt, że suma miar kątów przy tym samym ramieniu trapezu wynosi 180 stopni, a tutaj te kąty znajdują się przy podstawie, więc ta własność trapezu nie działa.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A dlaczego twierdzisz, że AS i BS to dwusieczne ?