elfre44 122 wyśw. 26-12-2024 14:15

3.76 Kurczab


proszę o pomoc nie wiem jak napisać matematycznie ten dowód zamiast takiego opisu który nie jest do końca  dokładny nawet mi się wydaje, jak uogólnić ten zapis matematycznie (te rysunki i pod to tylko sprawdzałam sobie jak wygląda)

planimetria Kurczab dowodzenie Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 28-12-2024 17:13

Jeżeli przez W oznaczymy kolejne wierzchołki np.

{W1, W2, W3, ... , W2n} - zbiór wierzchołków wielokąta gdzie n>=2

Oraz narysujemy wszystkie kąty środkowe  to powstanie nam 2n trójkątów równoramiennych.


Teraz możemy rozpisać po kolei kąty wewnętrzne wielokąta (ogólnie) oraz policzyć kąty przy wierzchołkach nieparzystych oraz parzystych i pokazać, że są one równe.

Artur 31-12-2024 15:35

Czyli tych trójkątów z tego co rozumiem to jest tyle ile wierzchołków ma wielokąt. Ale nie rozumiem jak rozpisać te kąty środkowe :/

jarosinski 01-01-2025 23:57

Tak zgadza się. 

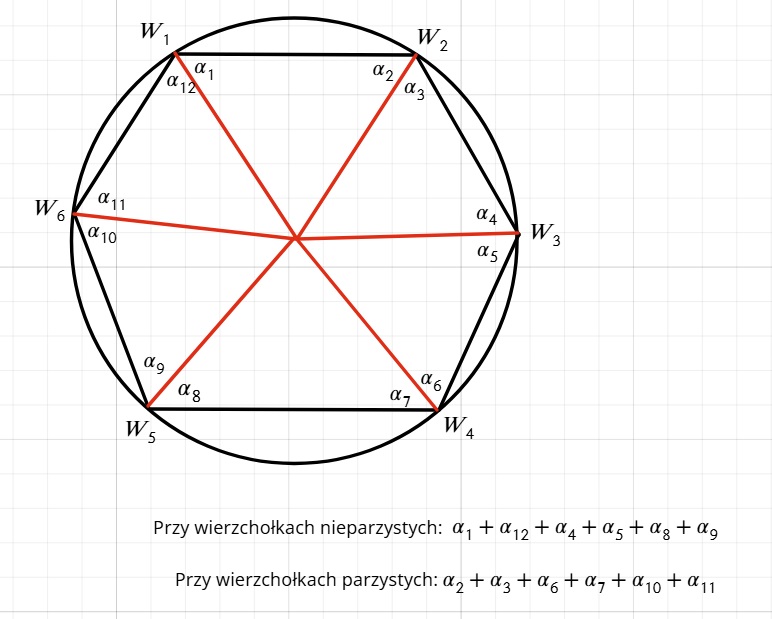
Tak wygląda przykładowy rysunek dla konkretnie: 6 wierzchołków. Widzimy, że powstaną nam trójkąty równoramienne. Pozostało teraz zgeneralizować rozwiązanie do "n" wierzchołków.



Artur 02-01-2025 19:17

Czy taki dowód byłby prawidłowy?

I czy ten wielokąt musi być foremny czy niekoniecznie?

jarosinski 03-01-2025 19:06

2. Nie musi

1. Bardziej formalnie byłoby:


Artur 04-01-2025 19:06

Dziękuję :)