Inf.17.

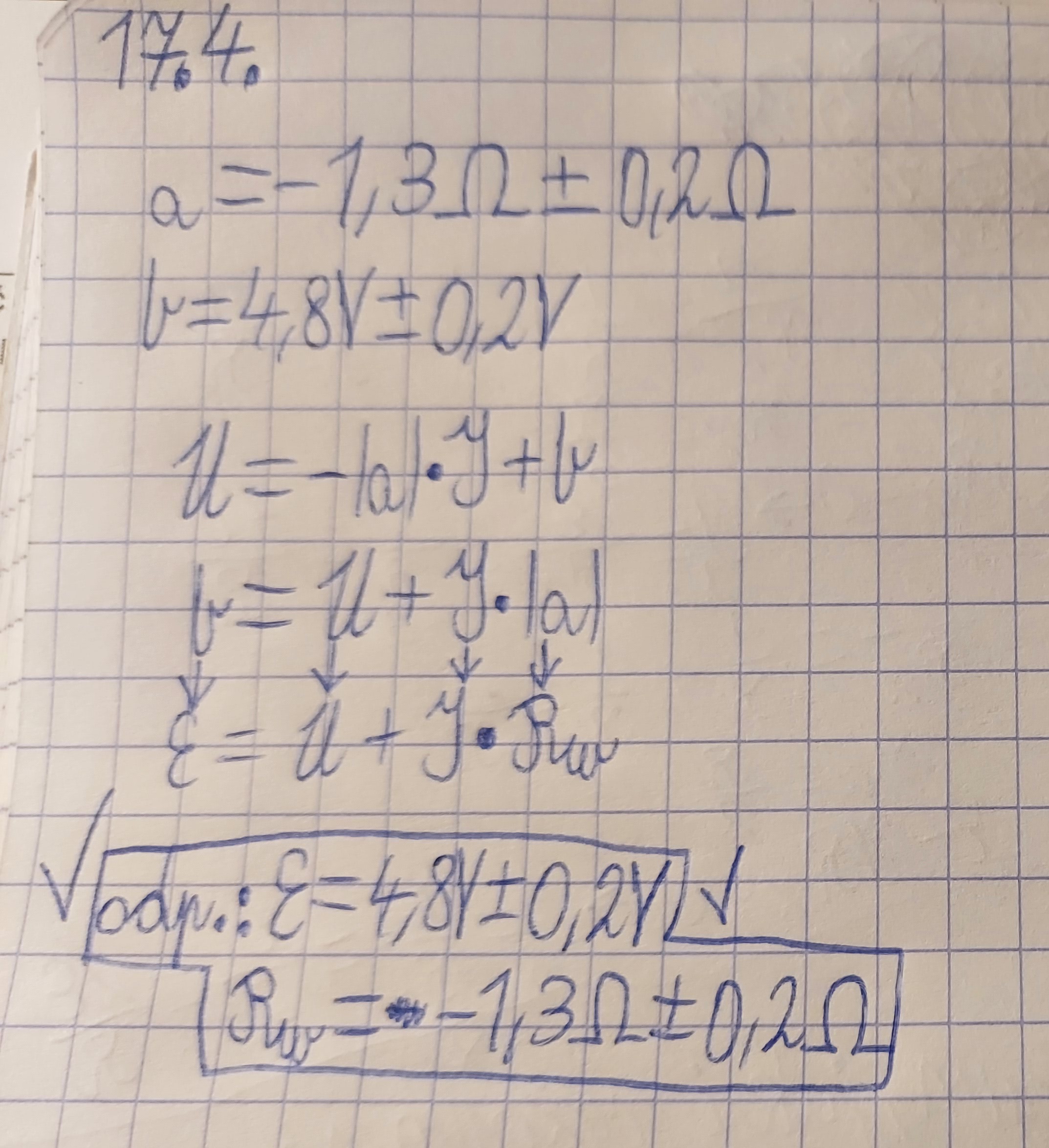
17.1.: Czy takie słowne uzasadnienie jest poprawne?
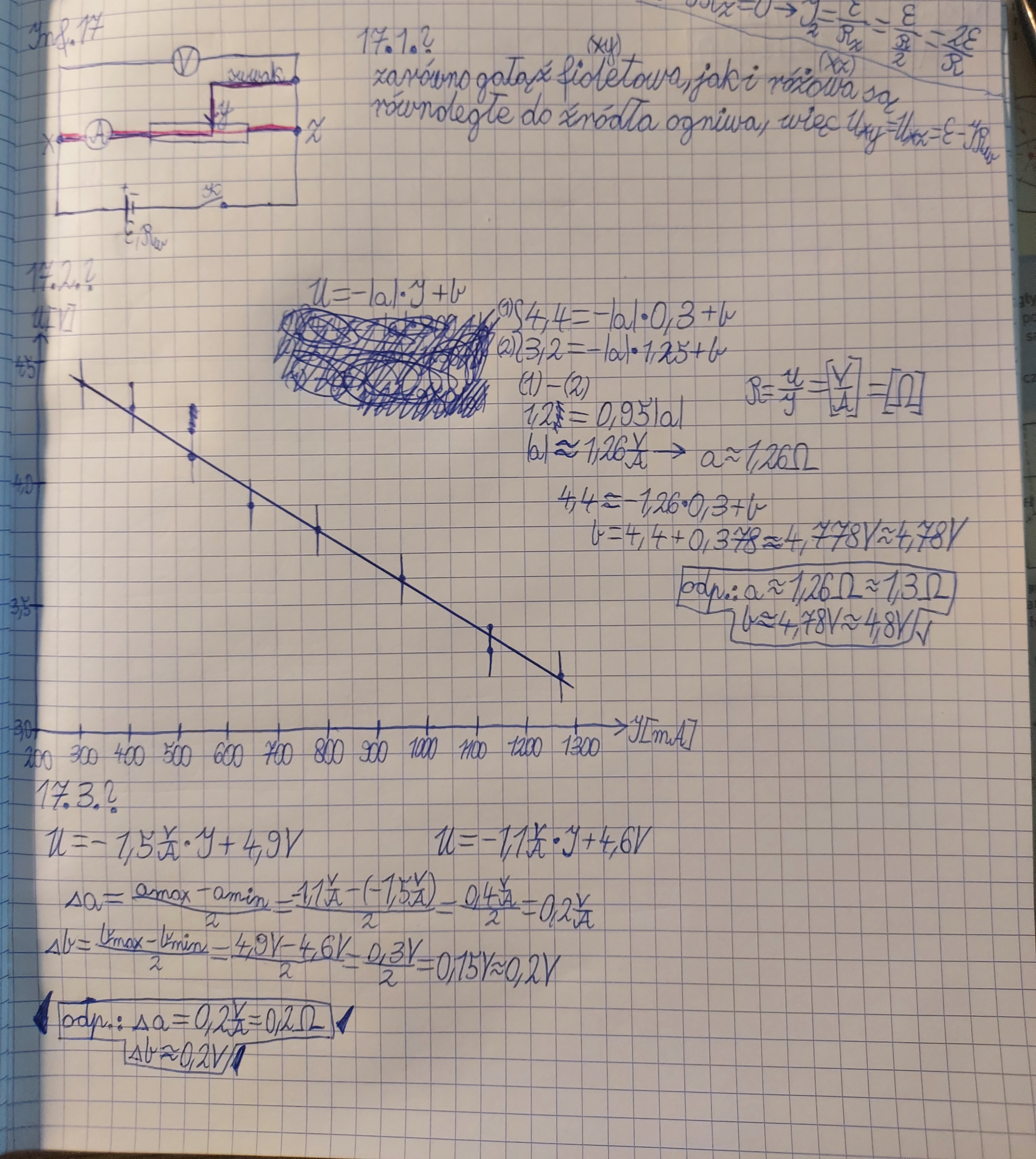
17.2.: Dlaczego w odpowiedziach "a" jest ujemne skoro to jest opór to powinien być dodatni i analogicznie w 17.4. jeśli w 17.2 napisali, że opór jest ujemny to w 17.4 też powinien być ujemny
17.3. Czy te wartosci są poprawne?
Fizyka prąd stały Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
17.1.: Ale w sumie skoro opór suwaka jest zerowy a opornika jest niezerowy, to nie wiem czy można napisać, że potencjał w punkcie Z jest taki sam jak w punkcie powyższym.
17.2.: No dobrze to opór wewnętrzny tak na logikę jest dodatni. Ale skąd mam wiedzieć czy "a" jest dodatnie czy ujemne skoro jest wzięte w wartość bezwzględną?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
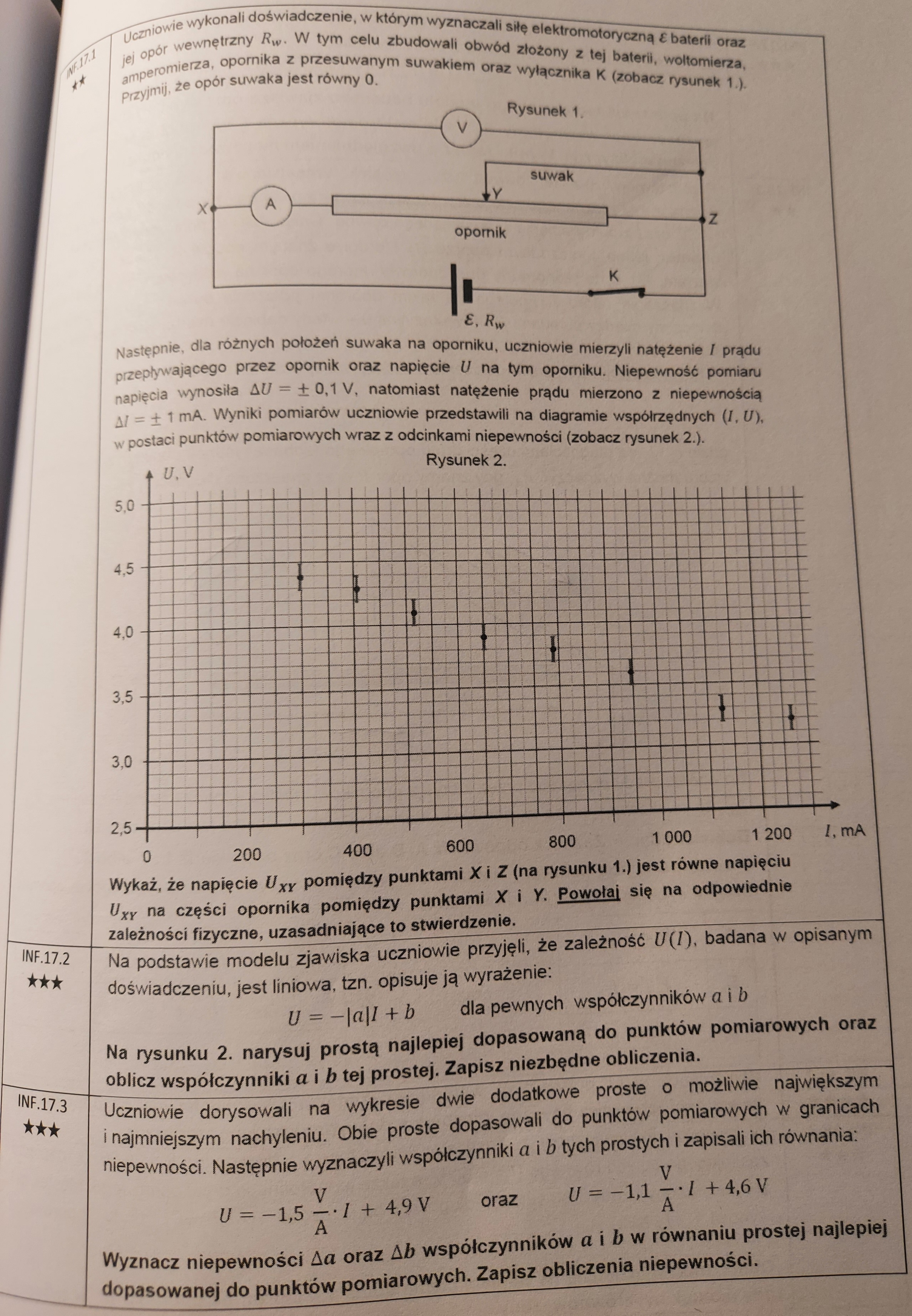
17.1 - wynika to wprost ze schematu przedstawionego w zadaniu. Pomiędzy tymi dwoma punktami po prawej stronie nie ma żadnego innego elementu, tylko fragment przewodu, którego opór jest zerowy, więc potencjały tych punktów są takie same.
17.2 - No w sumie to przy tak podanym wzorze w poleceniu to nie da się jednoznacznie rozstrzygnąć jaki znak ma a, skoro tam jest wrzucona po prostu jego wartość bezwzględna. Więc gdyby w odpowiedzi napisało się, że a jest dodatnie to też musiałoby to zostać uznane. Natomiast twórcy zrobili to zapewne w ten sposób po to, żeby wyraźnie zwrócić uwagę na fakt, że zależność U(I) jest ewidentnie funkcją malejącą.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale jeśli chodzi o odcinek YZ to jest tam jeszcze jakaś część tego opornika, więc opór na odcinku YZ nie jest równy zeru.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale tam prąd nie płynie - całość prądu płynie przez suwak, bo jego opór jest zerowy.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Czyli trzeba założyć, że opór RYZ jest nieskończenie duży? Bo mówi się, że prąd płynie tam, gdzie jest mniejszy opór, ale z drugiej strony przy różnych oporach przepływa przez oba oporniki połączone równolegle, więc chyba nie będzie płynął tylko tam, gdzie opór jest nieskończony (w przybliżeniu).
I wtedy takie coś co napisałem byłoby ok?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Właśnie nie - wystarczy, że przyjmiemy, że opór suwaka jest zerowy. Bo faktycznie w równoległym połączeniu dwóch oporników prąd rozdziela się tak, że stosunek prądów płynących przez gałęzie jest równy stosunkowi odwrotności oporów tych gałęzi (wynika to chociażby z II prawa Kirchhoffa). Czyli prąd będzie w całości płynął przez jedną gałąź jeśli stosunek oporów będzie równy 0 (lub nieskończoność, w zależności od tego jaki weźmiemy stosunek). A tak będzie wtedy gdy jeden z oporów będzie nieskończony, a drugi dowolny, ale skończony lub gdy jeden z oporów będzie zerem, a drugi dowolny, ale nie zerowy. W obu przypadkach bowiem stosunek wynosi nieskończoność (lub 0). I tutaj mamy do czynienia właśnie z tą drugą sytuacją.
I tak, to co napisałeś jest ok.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A no i teraz to ma sens. A gdyby np. połączyć równolegle coś o oporze zerowym i coś o oporze nieskończonym (lub 2 zerowe lub 2 nieskończone) to działałoby identycznie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
2 zerowe - tu już zależałoby od tego jak "bliskie" zera są oba te opory, jeśli byłyby identyczne, no to prąd podzieli się po równo. Dwa nieskończone opory - prąd w ogóle nie popłynie. Zerowy i nieskończony - cały prąd popłynie przez zerowy opór.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
17.1 - jest to ok, choć wynika to z faktu, że tak naprawdę punkt Z to jest ten sam punkt (czyli ma taki sam potencjał) co punkt znajdujący się zaraz nad nim. Więc tak dla 100% bezpieczeństwa dopisałbym tutaj takie jedno zdanie.
17.2 - ale opór to nie jest samo a, tylko wartość bezwzględna z tego a, czyli |a|. Tak zresztą jest to zapisane we wzorze U = -|a|*I + b z treści zadania. Więc wszystko jest ok, skoro opór wewnętrzny to |a|, to jest to jak najbardziej coś dodatniego.
17.3 - tak, jest ok.