Pr. Domowa 14 zad. 5

Zrobiłam to zadanie w ten sposób, ale w kryteriach jest zupełnie inne rozwiązanie, więc zastanawiam się, czy mam je komlpetnke nieprawidłowo zrobione. Proszę o odpowiedz.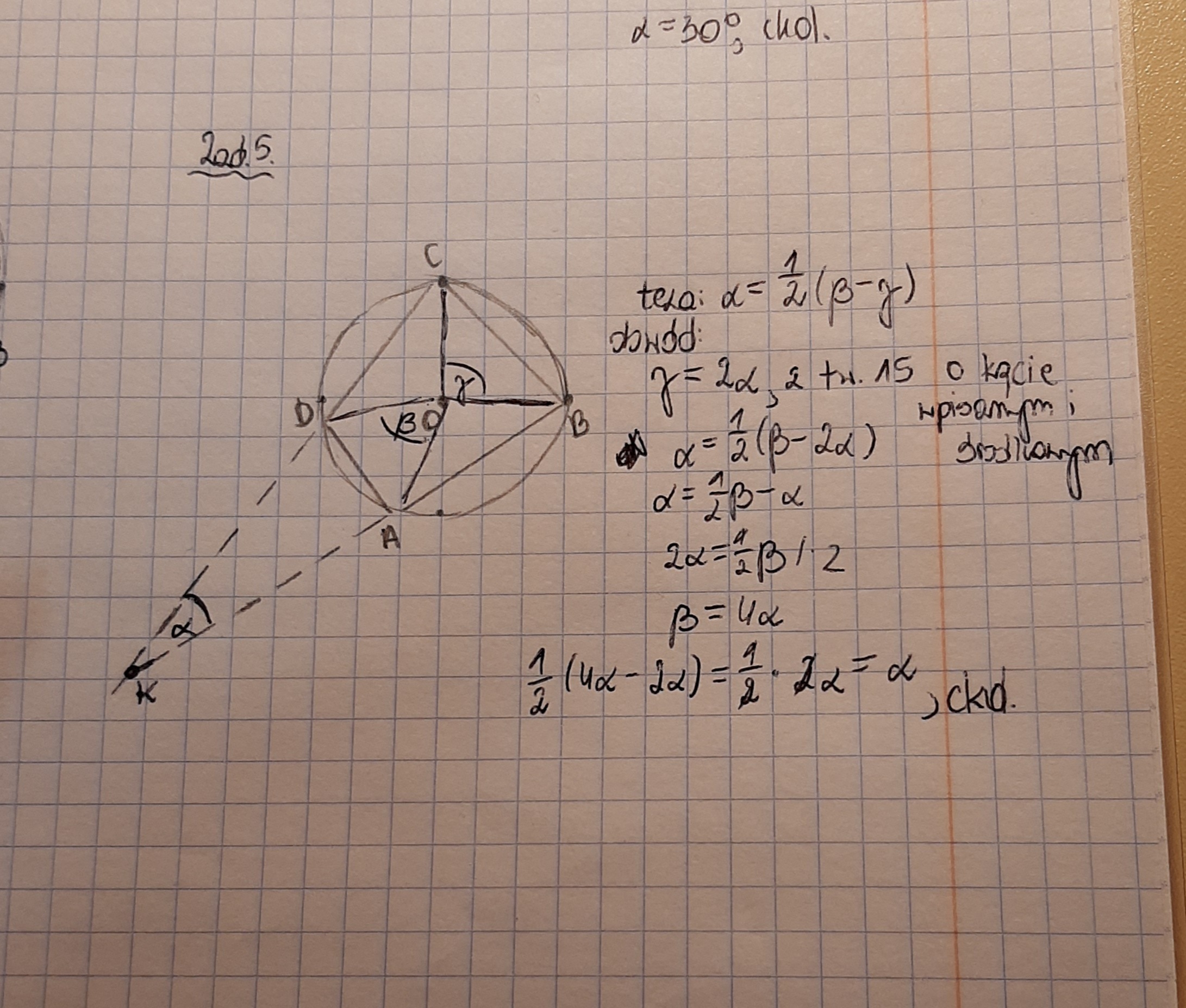
Planimetria Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Faktycznie, a mogę prosić o poprawne rozwiązanie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Trójkąty AOB, BOC, COD, DOA są równoramienne (ramionami jest
promień okręgu opisanego na czworokącie ABCD). Zatem w każdym z tych trójkątów,
kąty przy podstawie są równej miary (ale kąty przy podstawie jednego trójkąta
nie muszą być tej samej miary co kąty przy podstawie kolejnego trójkąta).
Spróbuj uzależnić miarę kąta przy podstawie od miary kąta przy wierzchołku O
(środek okręgu) w każdym z tych trójkątów, korzystając z sumy miar kątów
wewnętrznych w trójkącie. Następnie, korzystając z własności kątów przyległych
|∢CDO| + |∢ODA| + |∢ADK| = 180° oraz |∢OAB| + |∢OAD| + |∢DAK| = 180° można wyznaczyć miary kątów |∢ADK| i |∢DAK|,
a za |∢CDO|, |∢ODA|, |∢OAB|, |∢OAD| podstawić wyrażenia wyznaczone wcześniej z trójkątów
równoramiennych. Na końcu z sumy miar kątów w trójkącie DKA można już wyznaczyć |∢DKA|. (Dodatkowo: |∢AOD|+|∢AOB|+|∢BOC|+|∢COD|=360°)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
α to nie jest kąt wpisany, ponieważ jego wierzchołek (punkt K) nie leży na okręgu. Zatem tutaj twierdzenie o kącie wpisanym i środkowym nie zachodzi.