Praca domowa nr 15 Zad 6 część 1

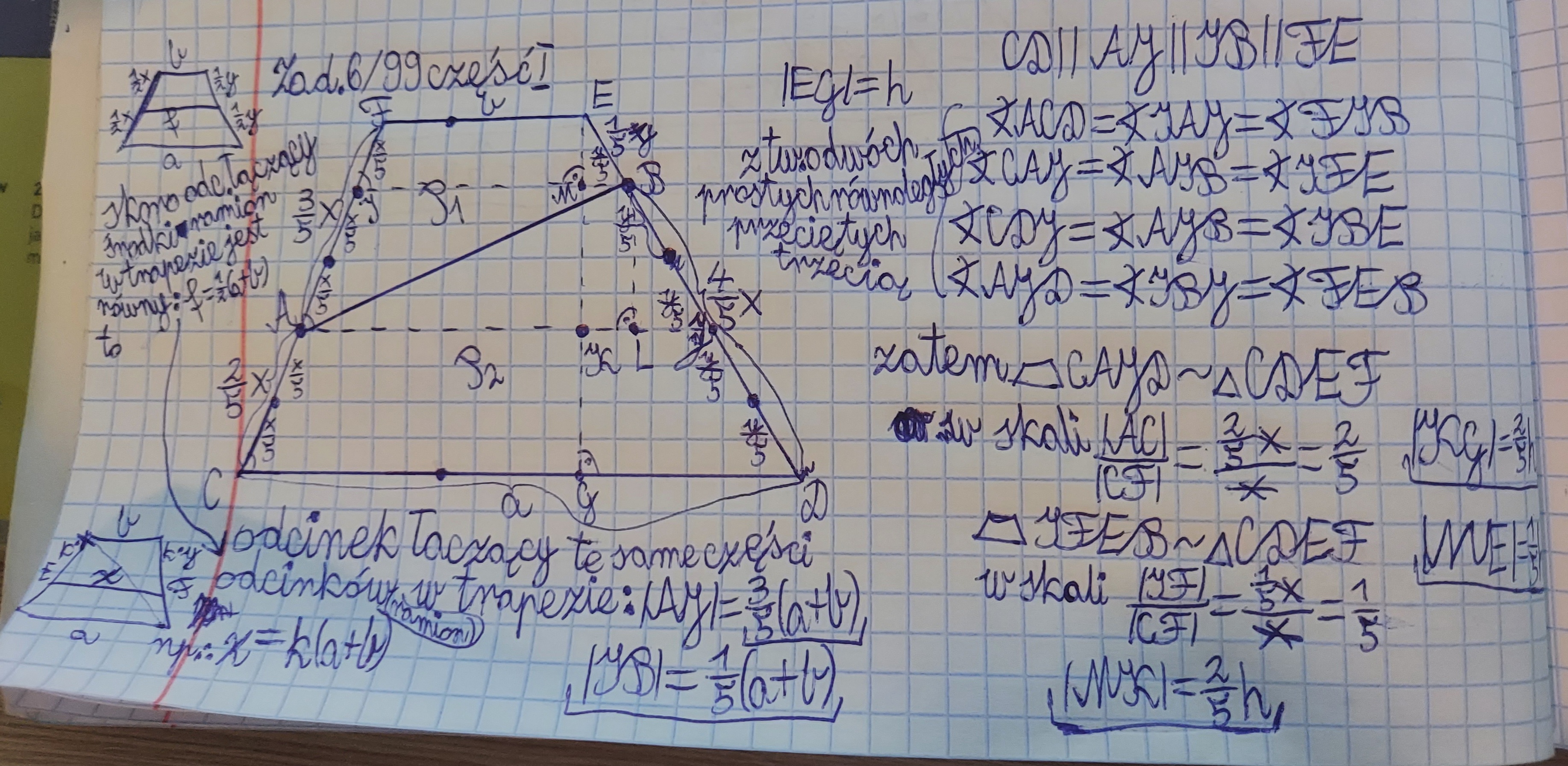

Dlaczego to rozwiązanie jest błędne?
Matematyka podobieństwo i przystawanie Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Rozumiem, że chodzi o pierwszą stronę rozwiązania. A więc:
1. krok: analiza kątowa (poparta twierdzeniem o dwóch prostych równoległych przeciętych trzecią)
2. krok: zauważenie podobieństwa trapezów CAJD, IFEB oraz CDEF
Oznaczając EG=h wychodzi ze skali, że: KG=2/5h=MK oraz EM=1/5h
3. krok: stwierdzam (nie wiem czy poprawnie), że analogicznie do wyznaczenia długości odcinka łączącego środki ramion w trapezie można wyznaczyć długość dowolnego odcinka łączącego ramiona w trapezie (szczegółowo opisałem to po lewej stronie i poniżej głównego dużego rysunku)
4. krok: Obliczenie P1=P CAJD + P APJ
P2=P IFEB + P AIB
Wynik jest niedaleki od poprawnego, dlatego uważam, że sposób może być poprawny, bo "a" w liczniku i w mianowniku wyszło mi dobre.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Którym wierzchołkiem u ciebie jest wierzchołek J ? Nie czytelne jest to na rysunku.
Napisałeś, że opisałeś to "twierdzenie" pod rysunkiem.
Nie jest one jasne i nie wiadomo co oznacza:
"Skoro odcinek łączący środki ramion w trapezie jest równy 1/2 * (a+b)
to odcinek łączący te same części (?) odcinków ramion w trapezie ?"
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Punkt J jest na prawym boku na tej samej wysokości co punkt A na lewym boku. A z tym odcinkiem łączącym te same części odcinków w trapezie to chodzi mi o to, że jak obierzemy 2 punkty na ramionach trapezu i połączymy je i powstanie odcinek równoległy do podstaw to jego długość będzie równa połowie sumy części odcinków ramion trapezu liczonych jakby powyżej tych punktów. Lepiej obrazuje to przykład: na powyższym rysunku zgodnie z przyjętymi oznaczeniami i moją obserwacją wychodziłoby, że: IP=0,2*(a+b) i analogicznie AJ=0,6*(a+b). No ale nie wiem czy jest to poprawne
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
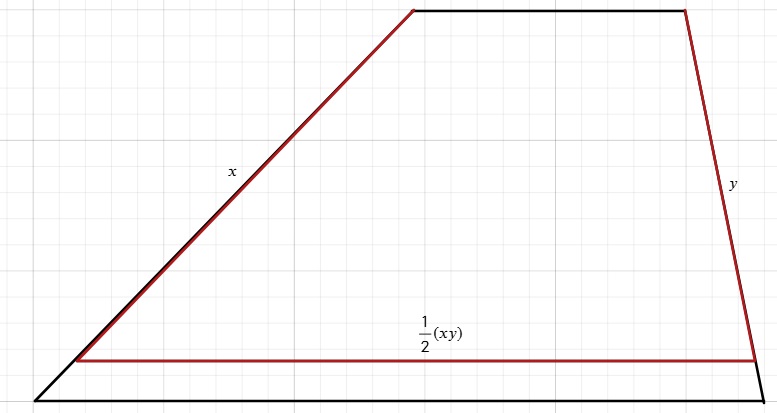
Masz na myśli coś takiego ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To będzie działać tylko gdy k = 1/2
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ten dowód polega na tym, że suma odcinków łączących środki boków trójkątów da środkową trapezu? Czyli rozumiem, że opiera się to po prostu na odcinkach łączących środki boków w trójkącie i gdy punktami nie będą środki ramion to proponowana przez mnie równość nie zajdzie i żadna zależność podobna do niej także.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W przypadku takiego trapezu nie zajdzie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
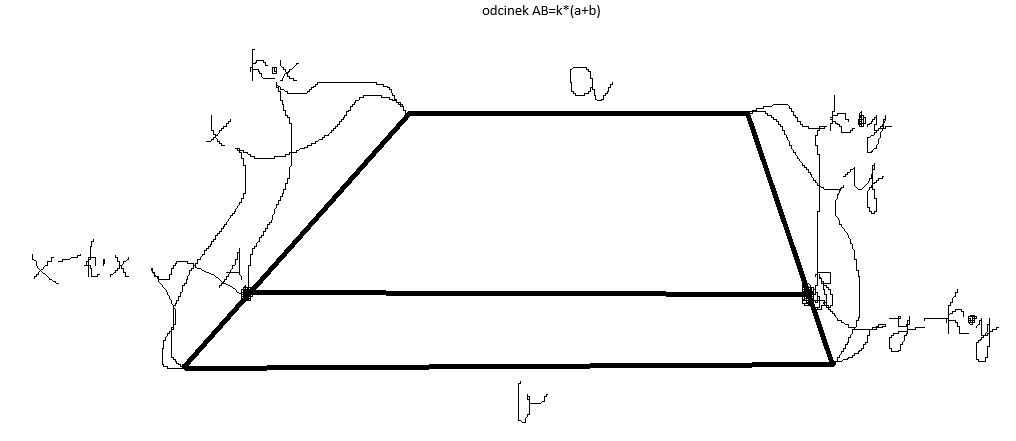
Rozwiązanie jest bardzo nieczytelne. Czy mógłbyś przepisać je pisząc krok po kroku i oznaczając kolejne punkty rozwiązania numerami. Zapisujesz kroki losowo w różnych miejscach przez co trudno jest odczytać jakie czynności wykonujesz po kolei.