igaxv 98 wyśw. 12-01-2025 17:53

3.74


Czy ktoś wie jak przeprowadzić ten dowód? Wiem, że tak jest, ale nie umiem tego rozpisać 

Matematyka dowód Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Maria 13-01-2025 12:36

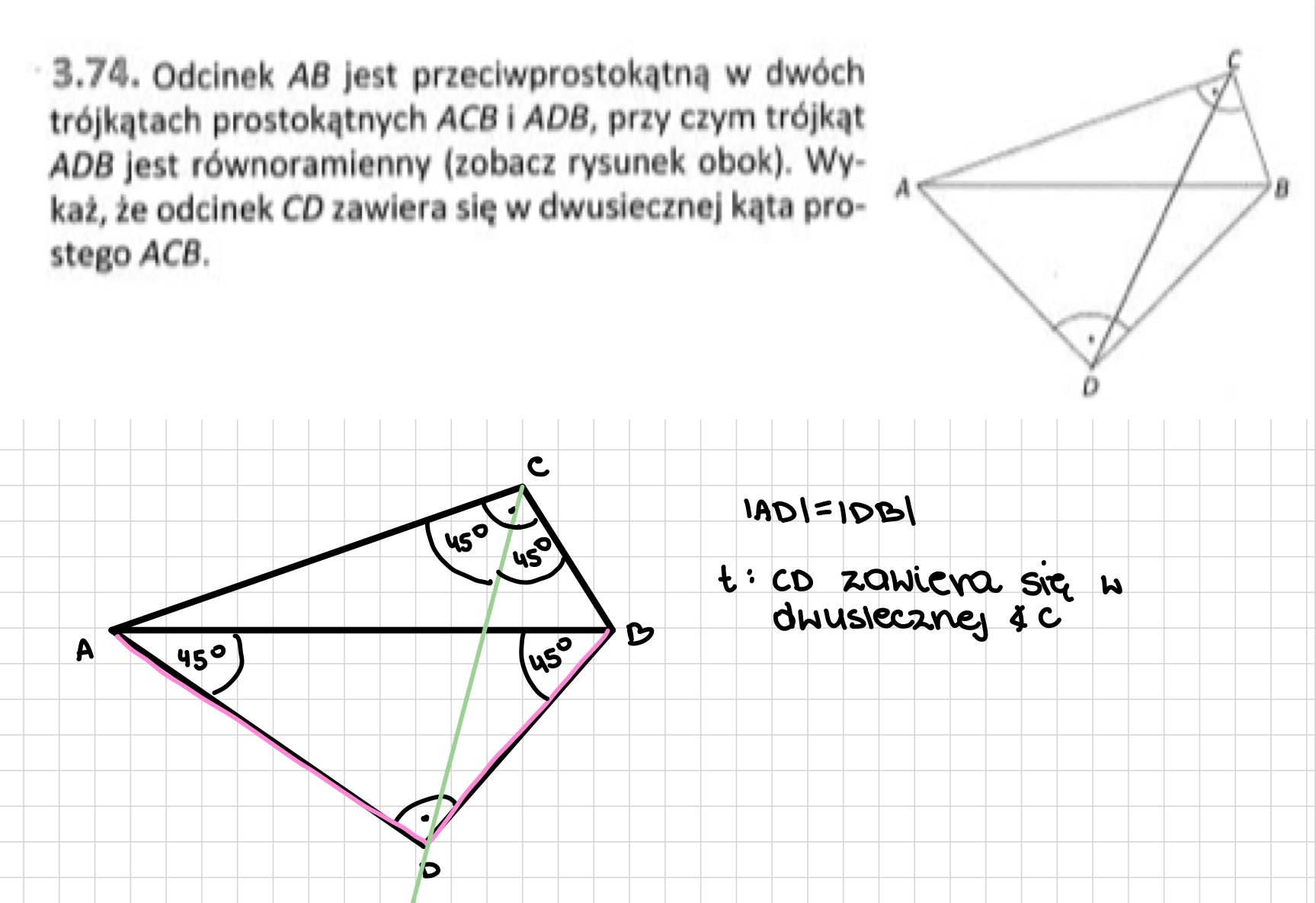
Najpierw warto udowodnić, że na czworokącie ADBC można opisać okrąg (sumy miar przeciwległych kątów są równe i muszą wynosić 180°). A potem już z kątów wpisanych wynika, że |∡ABD|=|∡ACD|=45° i |∡DAB|=|∡DCB|=45°, zatem |∡ACD|=|∡DCB|, więc CD zawiera się w dwusiecznej ∡C.