Zadanie domowe 15 cz. I, Zad 4

---

Hejka! Mam pytanie odnośnie zadania domowego nr. 15, cz I, zadanie 4.

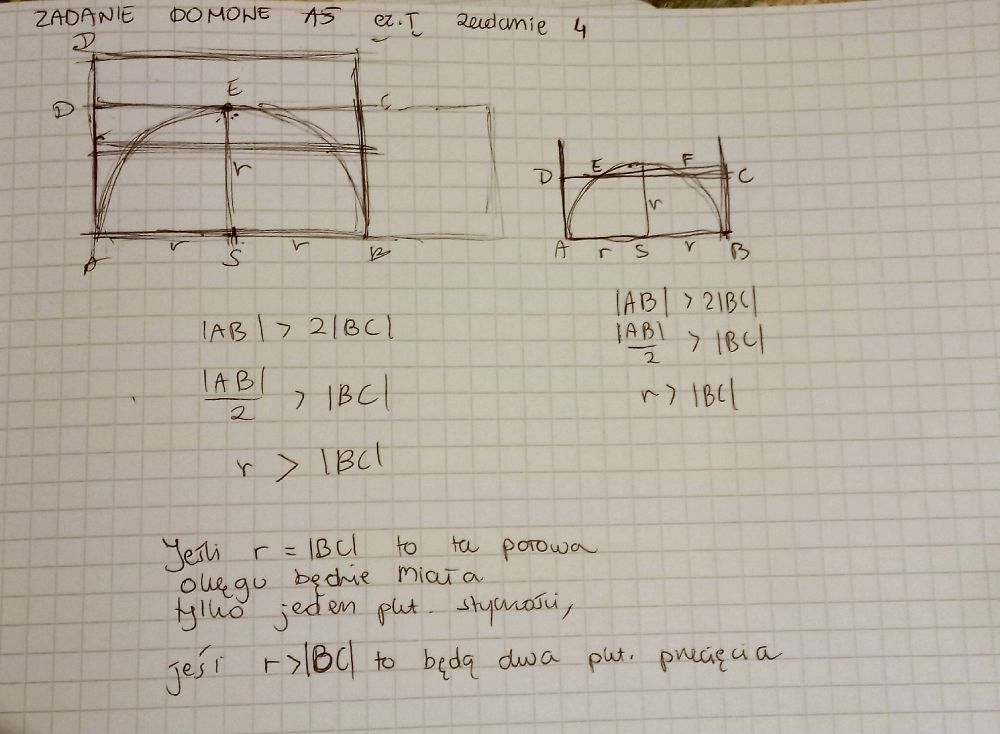
Jeśli ½|AB|>|BC|, czyli r>|BC|, to chyba muszą być dwa punkty przecięcia, a nie tylko punkt E? Bo tak się zastanawiam i nawet nie wiem jak ruszyć zadanie, bo wydaje się być sprzeczne. Może coś źle przekminiłam, no ale wydaje mi się że byłby jestem punkt przecięcia gdyby to |AB|=2|BC|, a w momencie gdy |AB| > 2|BC|, to mamy dwa pkt przecięcia.

Treść zadania: w prostokącie ABCD poprowadzono łuk okręgu o promieniu |AS|=|BS| i środku w punkcie S, który jest środkiem boku |AB| (|AB| > 2|BC|). Łuk ten przeciął bok |DC| w punkcie E. Udowodnij, że kwadrat o boku |BC| ma takie samo pole jak prostokąt którego boki mają długość |AC| i |DE|.

---

Matematyka planimetria przystawanie podobieństwo Dodaj post do ulubionych Poproś o pomoc