2017.8.


W rozwiązaniu sposobem drugim wychodzi mi, że aby dojść do tezy muszę wiedzieć, że a!=c (aby móc skrócić a-c). Czy takie założenie jest prawdziwe?
Matematyka planimetria Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A jak mógłbym to wykazać?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Prawidłowe podejście to rozważenie dwóch przypadków - raczej nie chcemy tutaj nic dowodzić na tym poziomie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No dobra no to dla a!=c powiedzmy, że mam już wykazane na powyższym zdjęciu. A jak dla: a=c?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeżeli a=c to trójkąt jest równoramienny i BE jest wysokością tego trójkąta.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
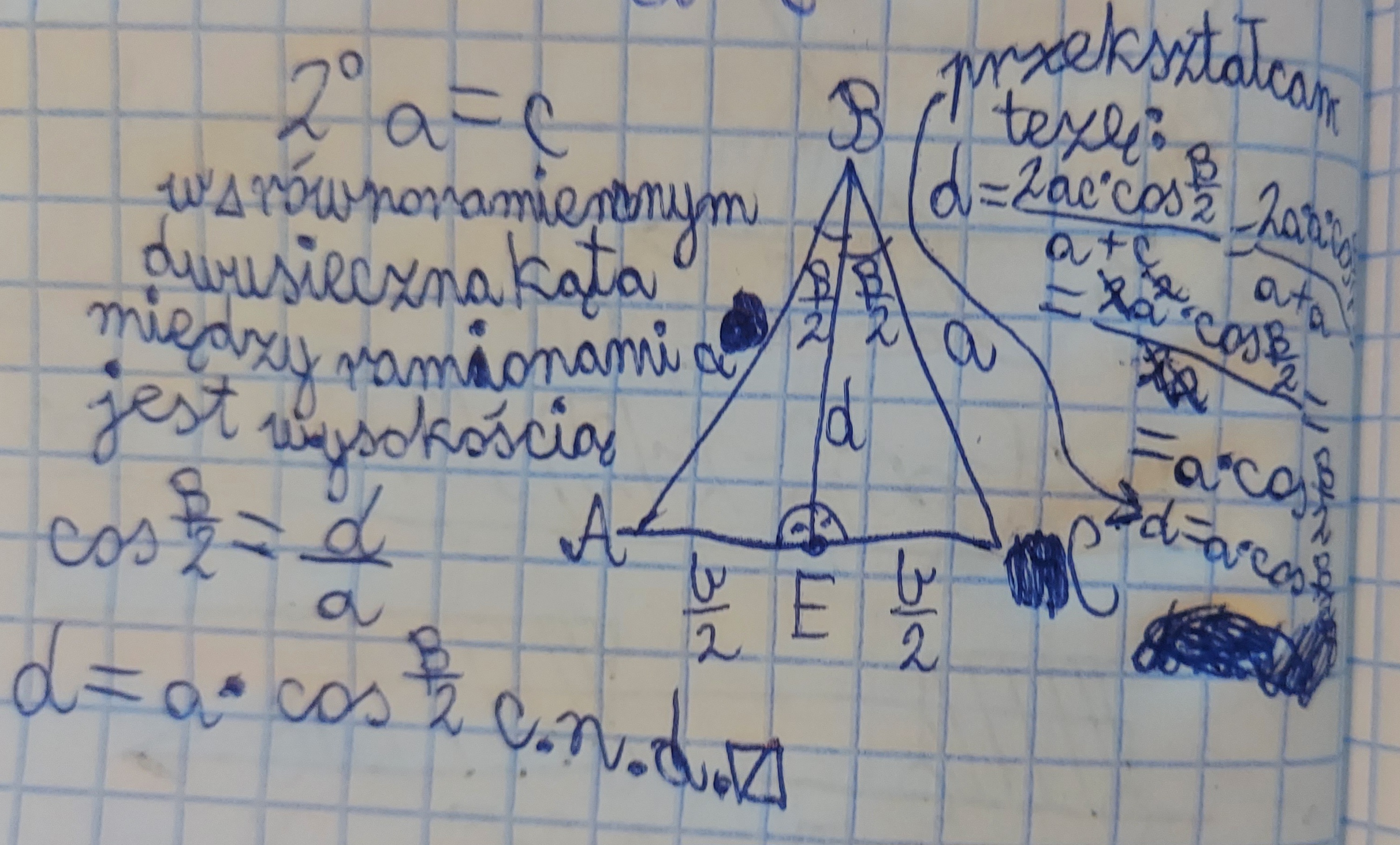
Czyli tak wyglądałby 2 przypadek?
Nie jestem pewny, czy dla jednego przypadku można sobie przekształcić tezę, a dla drugiego zostawić nieprzekształconą.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Polecam zerknąć do kryteriów, jak oni z tego wybrnęli:
https://szkolamaturzystow.pl/matury/matroz/2017%20maj%20nowa-odp.pdf
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Z tego co widzę to wychodzi na to, że można. Dziękuję :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeżeli chcesz skorzystać z tego założenia to musisz w jakiś sposób wykazać, że tak jest w przeciwnym razie będziesz dzielił przez 0.
A najlepsze rozwiązanie to rozdzielić na 2 przypadki: czyli zakładasz że a != c i rozwiązujesz do końca a następnie sprawdzasz co gdy a = c