Zadanie domowe 15 cz.1 zad.4
W prostokącie ABCD poprowadzono łuk okręgu o promieniu |AS| = |BS| i środku w punkcie S, który jest środkiem boku AB (|AB|>2|BC|). Łuk ten przeciął bok DC w punkcie E. Udowodnij, że kwadrat o boku BC ma takie samo pole jak prostokąt, którego boki mają długość |EC| i |DE|.
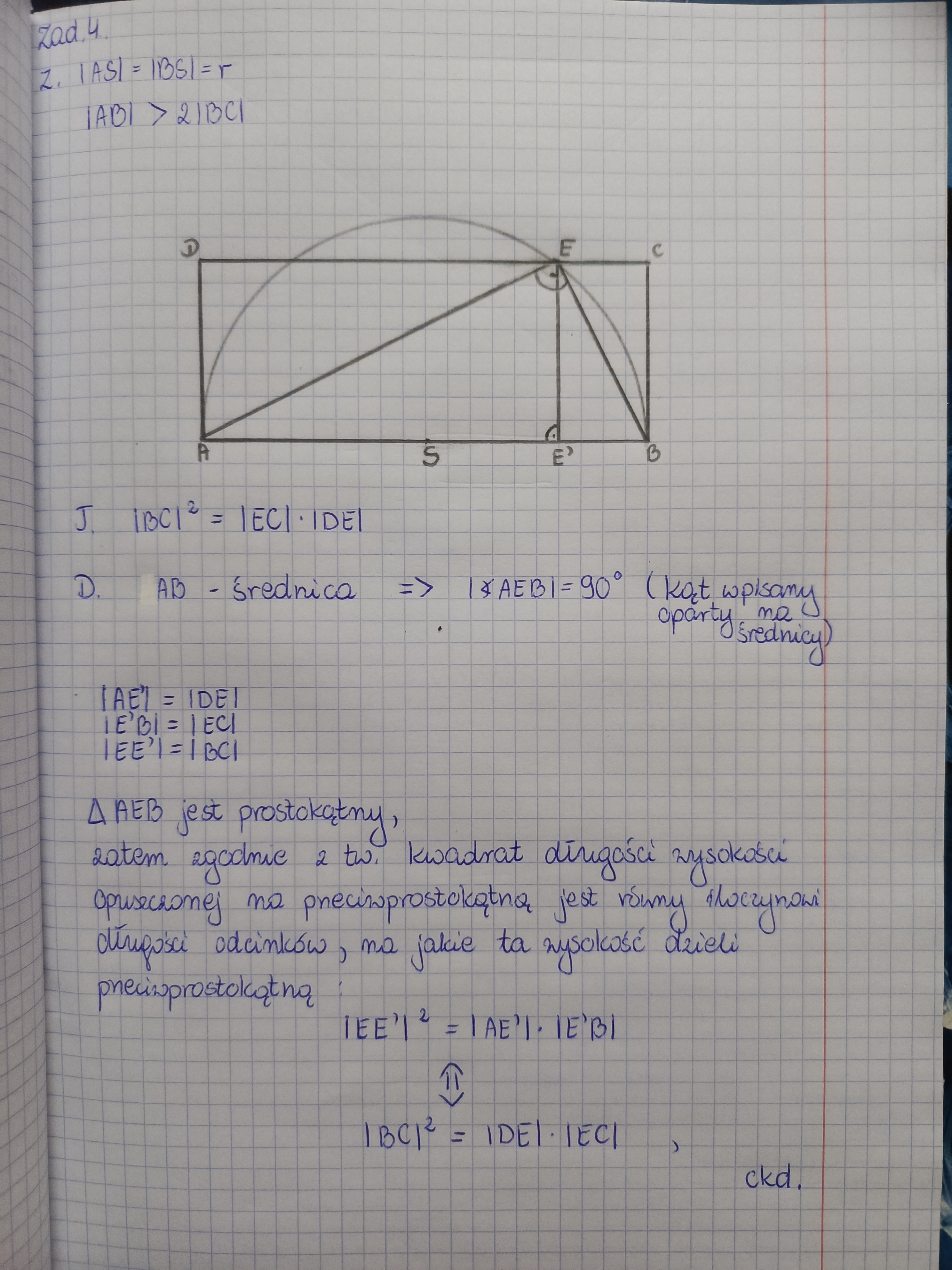
Czy takie rozwiązanie jest całkowicie dobre? Powołałam się tu na twierdzenie o wysokości opuszczonej na przeciwprostokątną i napisałam je słownie i nie wiem też czy może wystarczyłoby tylko napisać równanie? I czy powinnam dopisać też do tezy, że |BC|² to pole kwadratu o boku BC, a |EC|•|DE| to pole prostokąta o bokach EC i DE, czy tutaj też może zostać samo równanie?
Matematyka rozszerzona Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To twierdzenie/związek jest zapisany w kartach wzorów zatem możemy z niego skorzystać - zapisanie równania powinno wystarczyć, ale tak egzaminator wie, że korzystasz z twierdzenia. Teza jest ok.