2015.C.8
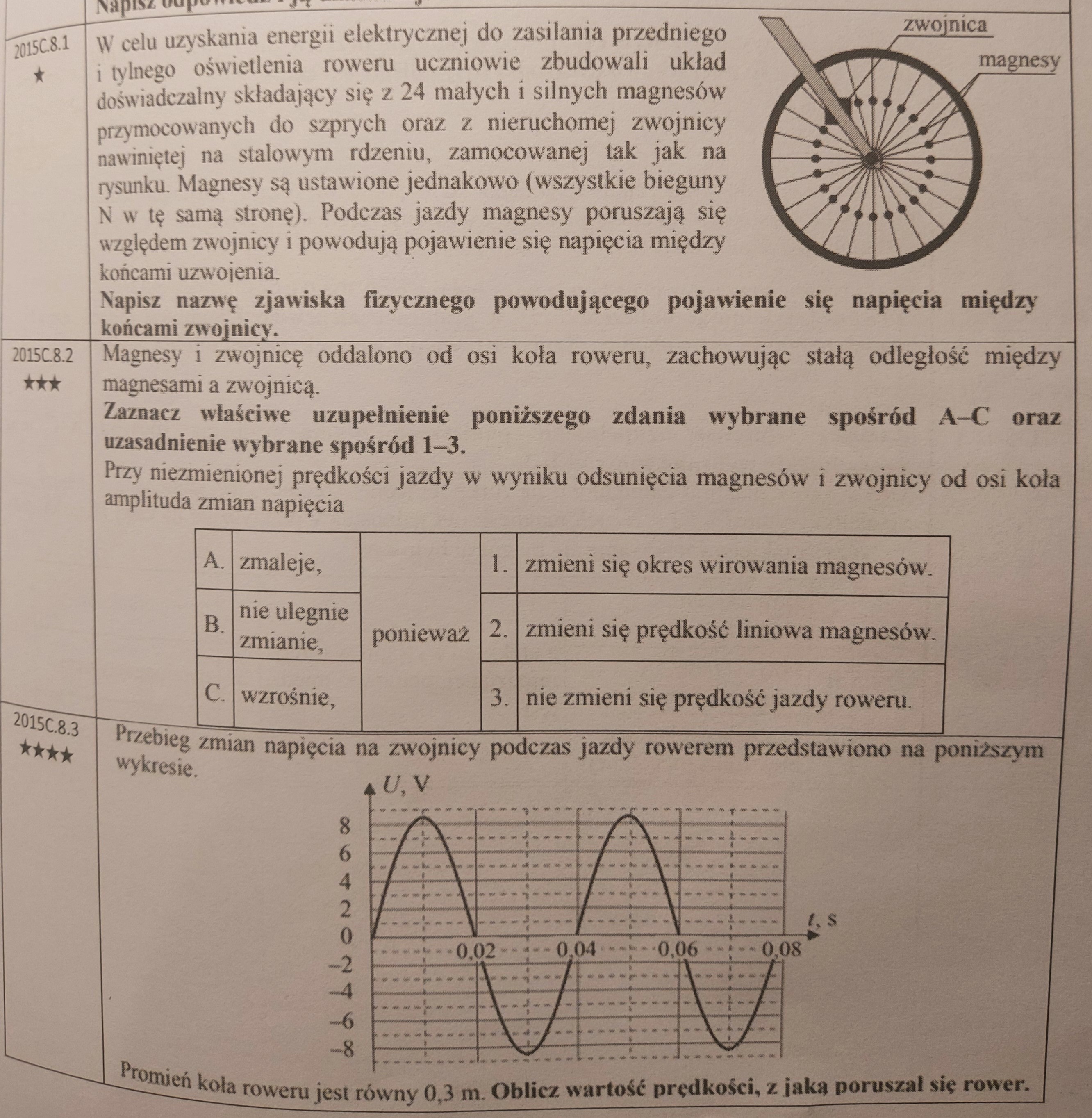

8.2.: Nie rozumiem jak dojść do poprawnej odpowiedzi. Próbowałem coś z wzorem U=BdV z poprzednich zajęć, ale chyba nie o to chodzi.
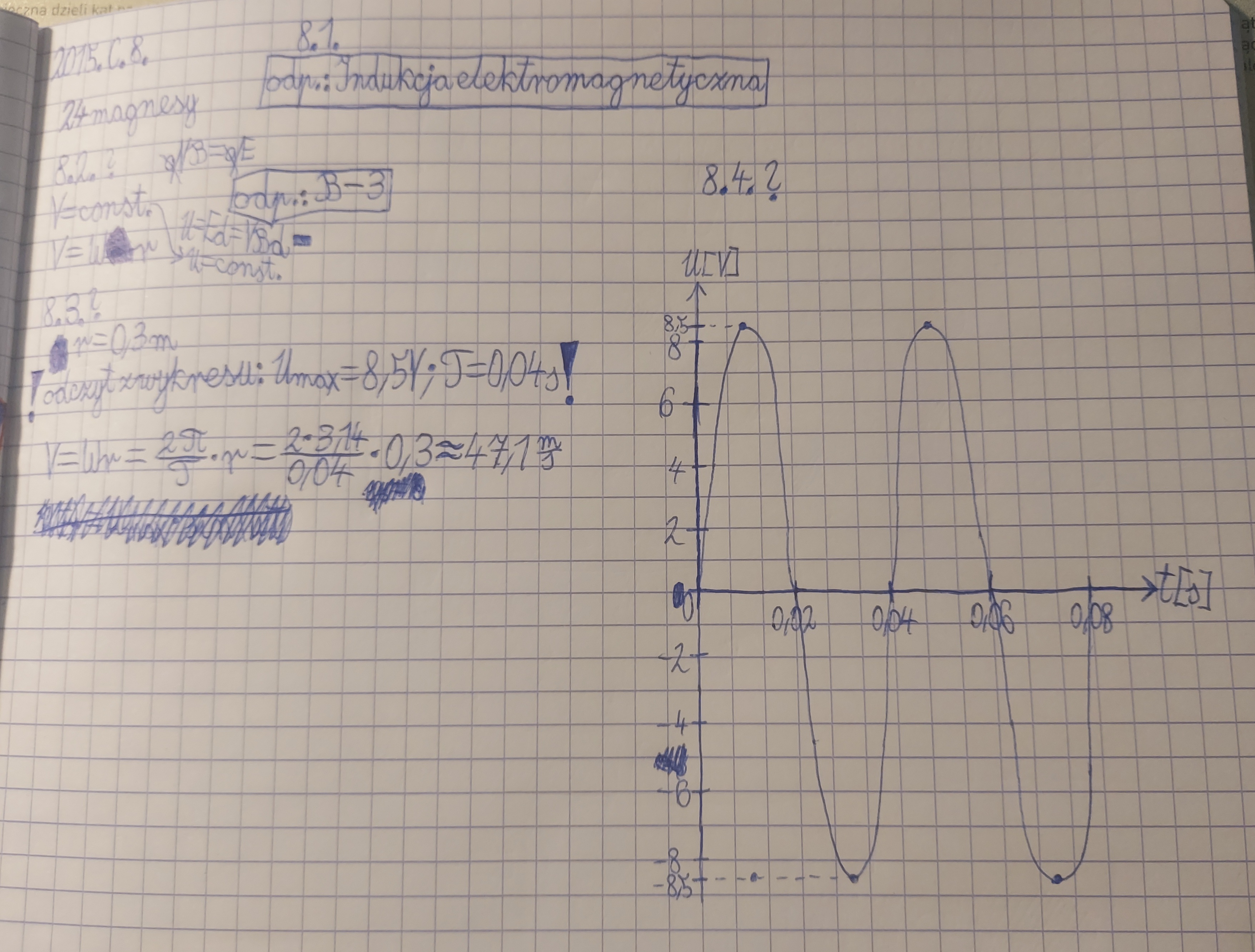
8.3.: Nie wiem dlaczego mój wynik należy podzielić przez 24. Przecież wykres zmian napięcia nie jest dla 1 magnesu. No a nie wiedząc jak obliczyć 8.3., nie wiem także jak zrobić 8.4., bo wydaje mi się, że jest to ze sobą powiązane.
Fizyka elektromagnetyzm Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
8.2.: No ale teoretycznie to im dalej od osi tym "wolniej" powinny przechodzić magnesy obok zwojnicy. I nie rozumiem powiązania prędkości liniowej roweru do prędkości magnesów, przecież skoro Vrower=const. to powinno być Vmagnes=const.
8.3.: Równie dobrze to 0,04s mogłoby być chyba okresem wszystkich magnesów, np. jakbyśmy skleili je taśmą.
8.4.: Rozumiem fakt, że okres wzrośnie dwukrotnie, bo to można wywnioskować ze wzoru V=2*pi*r/T, ale dalej nie rozumiem zbytnio tej zależności napięcia od prędkości.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
8.2 No nie, przecież jeśli mamy dwie sytuacje, w których rower porusza się z taką samą prędkością, ale w jednym przypadku magnesy są bliżej osi, a w drugim dalej, to w tym pierwszym przypadku prędkość magnesów względem zwojnicy będzie mniejsza, w drugim większa (punkty na obwodzie koła rowerowego poruszają się przecież szybciej niż punktu znajdujące się bliżej osi obrotu).
8.3 Przejście jednego magnesu obok zwojnicy powoduje powstanie jednego "impulsu" o kształcie sinusoidalnym. Czyli każdy taki okres zmian napięcia na zwojnicy odpowiada przejściu obok niej jednego magnesu. Okres obrotu koła odpowiada przejściu 24 takich magnesów, dlatego jest on 24 razy większy. Nie wiem czy do końca rozumiem sklejenie magnesów - tzn. tak, żeby wszystkie były hipotetycznie w jednym miejscu na kole? Jeśli coś takiego byśmy zrobili to amplituda napięcia by wzrosła, ale przejście takiej grupy magnesów obok zwojnicy dalej trwałoby około 0,04 s, a przez pozostałe 0,92 s te magnesy były na tyle daleko od zwojnicy, że nie indukowałoby się już w niej żadne napięcie (dostalibyśmy tylko jeden taki impuls). Co nie zmienia faktu, że okres obrotu koła dalej wynosiłby 0,96 s.
8.4: jak wspomniałem we wcześniejszym komentarzu przy pp nr 2, wynika to z prawa Faradaya - im mniejsza prędkość, tym mniejsza zmiana strumienia w takim samym przedziale czasu, tym mniejsze indukowane napięcie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
8.3.: Ale czy na tegorocznej maturze w takim przypadku nie powinno być napisane, że wykres przedstawia zależność napięcia od czasu przejścia jednego magnesu? Poza tym wydaje mi się to trochę bez sensu, bo wychodzi na to, że im więcej jest magnesów tym wolniej jedzie rower. Chyba, że one mają stawiać jakiś opór.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale ten wykres to nie jest wykres zależności napięcia od czasu przejścia jednego magnesu, tylko po prostu wykres zależności napięcia indukowanego w zwojnicy po prostu od czasu. A to, że akurat jeden "impuls" związany jest z przejściem obok zwojnicy jednego magnesu to już inna sprawa.
A drugiej części nie bardzo rozumiem - nie jest nigdzie powiedziane, że im więcej magnesów tym wolniej porusza się rower. Te rzeczy przecież są od siebie niezależne. Faktem jest, że prędkość roweru możemy obliczyć wiedząc, że tych magnesów jest 24, ale nie oznacza to wcale, że liczba magnesów ma jakikolwiek wpływ na prędkość roweru.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dalej nie rozumiem skąd mam wiedzieć, że T=0,04s to okres dla przejścia jednego magnesu, bo o żadnych impulsach też nie napisali w treści.
Co do drugiej części pytania to jeśli uznam, że T1=0,04s (T1-okres 1 magnesu) i wtedy V=(2*pi*r)/(n*T1), gdzie n-ilość magnesów (taki wzór wynika z odpowiedzi CKE) to wtedy im większa będzie liczba magnesów tym mniejszą prędkość będzie miał rower.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tę nazwę "impuls" wprowadziłem sobie sam, mając na myśli jedno pełne "drganie", czyli fragment sinusoidy odpowiadający jednemu okresowi. No bo wyobraźmy sobie sytuację, że jest tylko jeden magnes w jednym miejscu (na jednej szprysze, a reszta szprych koła nie posiada magnesów). Jak wtedy będzie wyglądał wykres zależności napięcia od czasu? Przez większość czasu napięcie będzie zerowe (bo magnes jest daleko od zwojnicy i nie ma żadnej zmiany strumienia indukcji przechodzącej przez zwojnicę, więc nie indukuje się w niej napięcie), a tylko w pewnym krótkim przedziale czasu to napięcie się wzbudzi - gdy magnes będzie przechodził obok takiej zwojnicy. I w dobrym przybliżeniu można uznać, że to wzbudzenie napięcia będzie miało kształt własnie takiego jednego "impulsu" sinusoidalnego, czyli od zera do maksimum w jedną stronę, potem do minimum (maksimum w drugą stronę) i znów do zera i potem znów przez dłuższy czas utrzymuje się zero, bo magnes już oddalił się całkiem od zwojnicy. I długość trwania tego impulsu to będzie właśnie ok. 0,04 s. Jeśli teraz ułożymy 24 takie magnesy obok siebie, żeby objęły cały obwód koła, to te impulsy będą się ciągle powtarzały, każdy trwając 0,04 s i stąd dostajemy taki przebieg napięcia na zwojnicy od czasu.
Druga część - ok, ale im większe dasz n, tym mniejszy będzie okres T1 dla każdego takiego magnesu. Tak, że finalnie iloczyn n*T1 będzie stały.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ma to sens, ale uważam, że z treści zadania nie wynika to wprost i powinni coś jeszcze dopisać, bo można pomyśleć, że 0,04s to okres obrotu całego koła. Chyba, że trzeba spojrzeć na to w ten sposób, że dla 1 magnesu 1 raz jest Umax i jeden raz jest Umin i dzieje się to w czasie 0,04s, więc jest to okres przejścia 1 magnesu. Takie rozumowanie jest dobre?
A z ciekawości dlaczego ten rower jedzie tak wolno? Bo mówiliśmy kiedyś o weryfikacji wyników i ta prędkość wydaje się dosyć mała jak na rower.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
"Chyba, że trzeba spojrzeć na to w ten sposób, że dla 1 magnesu 1 raz jest Umax i jeden raz jest Umin i dzieje się to w czasie 0,04s, więc jest to okres przejścia 1 magnesu. Takie rozumowanie jest dobre?"
Tak, można to tak interpretować :)
A że rower jedzie wolno - no cóż, faktycznie trochę wolno, ale nie jest to żaden absurdalny wynik ;) ale już np. uzyskany przez Ciebie pierwszy wynik jest zdecydowanie podejrzany - 47 m/s to prawie 170 km/h, więc gdyby coś takiego otrzymał na maturze to bardzo poważnie bym się zastanawiał czy nie popełniłem gdzieś błędu.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No to prawda. Dlatego też wiedziałem, że trzeba coś zrobić z ilością magnesów i mnożąc wyszłoby jeszcze więcej, a po podzieleniu wynik 1,96 m/s także wydał mi się dziwny, ale jak się okazuje poprawny. A gdyby nie napisać nic na temat związku okresu z przechodzeniem kolejnych magnesów i po prostu "na pałę" podzielić przez 24 (tak zrobiłem przed napisaniem pytania do tego zadania) to dostałoby się max punktów?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
8.2: Nie wyprowadzimy tutaj dokładnego wzoru na to jak wygląda zależność indukowanego napięcia od ruchu magnesów, ale wystarczy nam taka połowicznie ilościowa analiza. Mianowicie faktycznie im większa prędkość magnesu, który "przechodzi" obok zwojnicy, tym większa amplituda tego napięcia (wynika to z prawa Faradaya: Eind = deltaFi/deltat, czyli im szybszy ruch magnesu, tym większa zmiana strumienia Fi w jakimś przedziale czasu deltaT, tym większe indukowane napięcie). Jeśli zatem odsuniemy zwojnice i magnesy od osi obrotu, a rower będzie dalej poruszał się ze stałą prędkością, to oznacza to, że prędkość kątowa tych magnesów się nie zmieni, ale zmieni się ich prędkość liniowa w ruchu po okręgu, więc będą one przechodziły każdorazowo "szybciej" obok zwojnicy. Stąd C2 jest poprawną odpowiedzią.
8.3: Pozwolę sobie skopiować wytłumaczenie tego podpunktu z innego tematu na naszym forum: Zauważmy, że w istocie okres zmian napięcia na zwojnicy wynosi 0,04 s, natomiast nie jest to wcale okres obrotu dla naszego koła - a Ty wykonując takie obliczenie utożsamiłeś ze sobą te dwie wielkości. Należy się zastanowić z czego wynika okres zmian napięcia w zwojnicy - jest to związane z faktem, że obok niej "przechodzą" kolejne magnesy zamocowane na szprychach. A zatem jeden okres zmian napięcia odpowiada przejściu obok zwojnicy jednego magnesu - ponieważ zaś takich magnesów jest 24, to okres obrotu całego koła jest 24 razy większy od okresu zmian napięcia, czyli wynosi 0,96 s. Jeśli dla takiego okresu obrotu koła obliczymy prędkość roweru to uzyskamy już dobry wynik :)
8.4: Skoro teraz prędkośc roweru jest dwukrotnie mniejsza, to dwukrotnie mniejsza jest też prędkość z jaką każdy magnes przechodzi obok zwojnicy - a zatem amplituda zmniejszy się w dobrym przybliżeniu dwukrotnie, a okres zwiększy się dwukrotnie.