Zadanie domowe nr 10

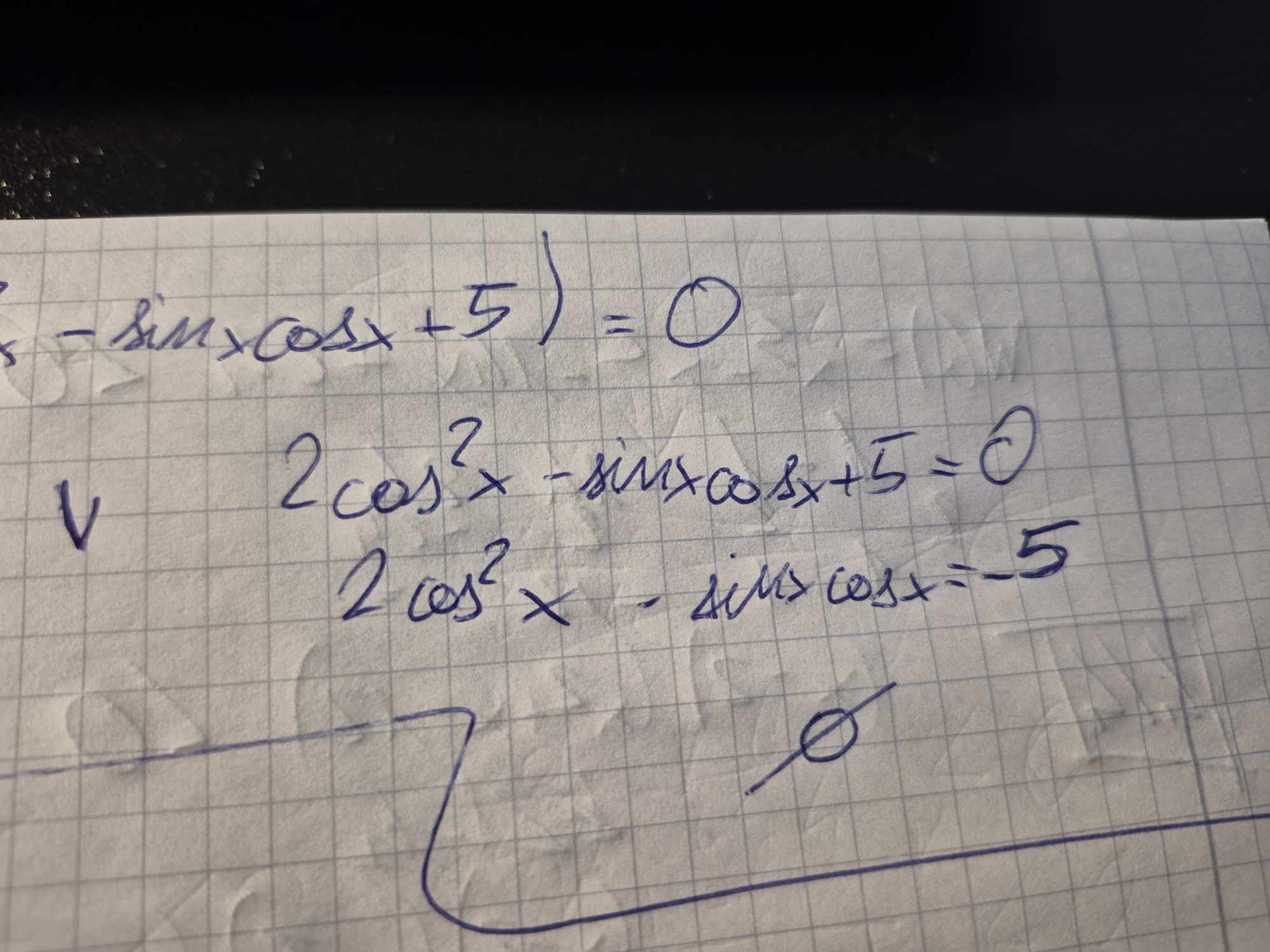

1) Czy poprawnie udowodniłem?
2) Dlaczego odrzucamy to równanie trygonometryczne, wiem że sin, cos mają zbiór wartości [-1,1] a tam jest -5, ale w równaniu są różne operacje na (sin, cos) takie jak (^2, -, *) dlaczego więc tak mamy założyć ?
3) Czy mogę to zadanie zrobić w ten sposób, jeżeli tak/nie dlaczego?
Matematyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
2) Dokładnie takie równanie znajduje się w odpowiedzi do tego zadania w Pana książce i takie mi też wyszło, nie rozumiem jedynie tej części odpowiedzi:
Zadałem również pytania 1) i 3) ponieważ w 1) zastanawia mnie czy mój tok rozwiązywania (udowadniania) zadania jako funkcji kwadratowej jest prawidłowy i czy wszystko jest napisane tak jak być powinno, w 3) rozwiązałem zadanie swoim wymyślonym sposobem i nie wiem czy taka operacja jest w ogóle dozwolona mimo że dowód wychodzi w teorii poprawny
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy mógłbyś wskazać fragment w książce w którym delta została zapisana tak jak u ciebie ? Jeżeli tak jest to jest to błąd.
Tak powinno to wyglądać:
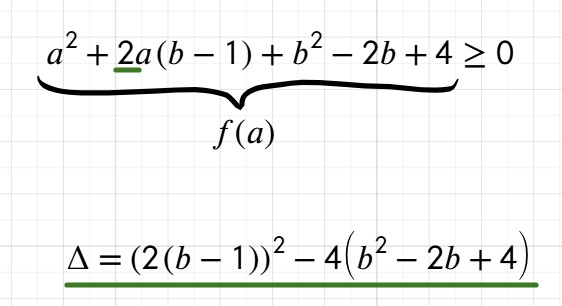
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeżeli chodzi o zbiór wartości:
Rozważmy ekstremalny scenariusz, który i tak nie może mieć miejsca dla:
2* cos^2(x)-sinx*cosx
2*cos^2(x) najmniejszą liczbą jaką może być to 0 natomiast
-sinx*cosx największą jaką może być to 1
Mimo że taka sytuacja nigdy jednocześnie by nie zaszła to nie możliwym jest aby dojść do -5
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeśli widzimy że jedna ze stron zawiera funkcje trygonometryczne a druga przesadnie małą/dużą wartość warto przez chwilę zastanowić się czy to jest możliwe.
Co do twojego rozwiązania 3.
Wykazałeś z nierówności, że x+y+z >= 3, natomiast jak to się ma do tezy:
(1+x)(1+y)(1+z)>=8 ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Błędnie wyliczyłeś deltę.
To równanie nigdy nie może być równe -5 mimo mnożenia przez 2 i kwadratu.