2024C.3.2

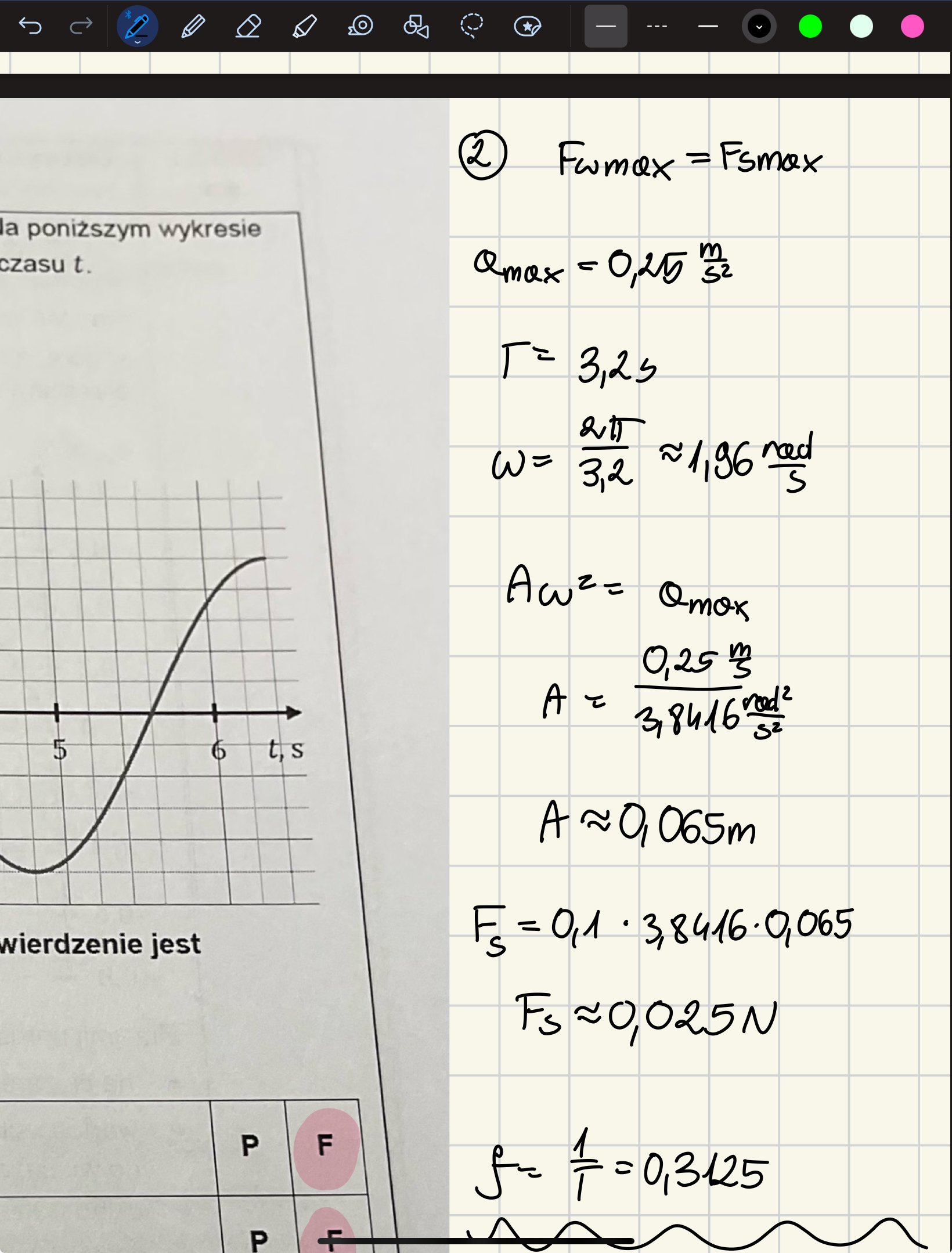
Zauważmy bardzo ciekawą rzecz, mianowicie w przypadku tego zadania nie wiemy nawet czy mamy do czynienia z ruchem ciała na sprężynie (w pionie/poziomie) czy też ruchem wahadła czy może w ogóle z jakimś innym rodzajem ruchu harmonicznego - jedyne co wiemy z treści to tylko tyle, że jest to ruch harmoniczny wzdłuż jednej osi x i wiemy jak wygląda zależność przyspieszenia tego ciała w ruchu harmonicznym od czasu (no i znamy jego masę).

A zatem nie wiemy nawet czy siła ciężkości ma tutaj jakiekolwiek znaczenie w ruchu tego ciała. Na szczęście ta wiedza w ogóle nie jest nam potrzebna, bo zauważmy, że nie pytają nas o siłę sprężystości Fs, ale po prostu o siłę wypadkową działającą na to ciało. A siła wypadkowa to zgodnie z II zasadą dynamiki zawsze jest Fw = m*a. I w przypadku ruchu harmonicznego Fw jest maksymalna zawsze w położeniach o największym wychyleniu (czy to w jedną czy to w drugą stronę). Tu wystarczy odczytać maksymalną wartość przyspieszenia jakie ma to ciało, bo skoro Fw = m*a, to Fw,max = m*amax. Odczytujemy zatem z wykresu amax i przemnażamy je przez masę ciałą i mamy maks. wartość siły wypadkowej.