ZZ.123

potrzebuję pomocy z pp3), 4) i 5)
matura Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czy jak chodzi o pp 3) tak jest okej? czy mam jeszcze coś zmienić lub dopisać z tymi niepewnościami ??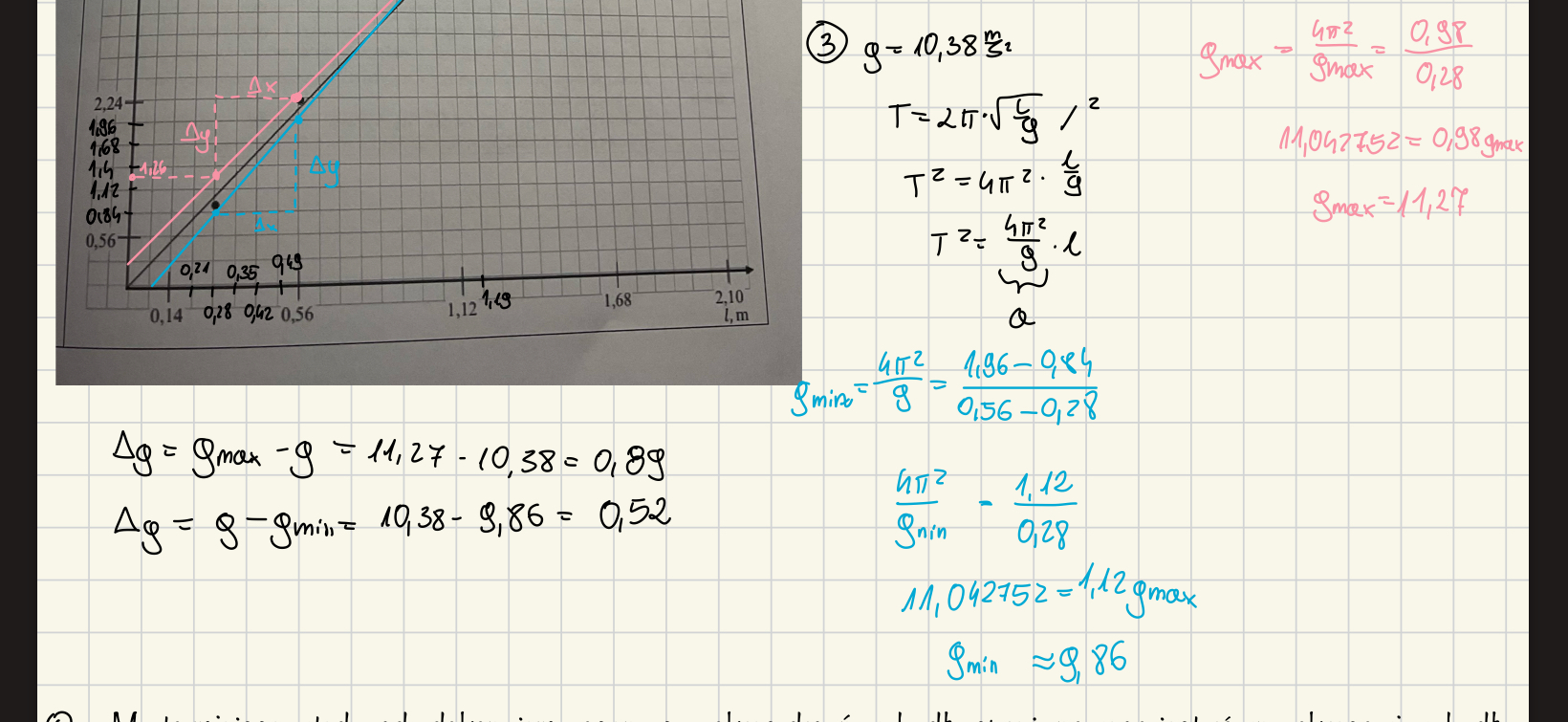
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak na dobrą sprawę to pasowałoby wyznaczyć jedną konkretną wartość tej niepewności bezwzględnej - zgodnie z treścią maksymalną, więc należałoby tu w sumie wybrać tę większą wartość. Przy czym w praktyce eksperymentalnej nie jest to jednoznacznie określona procedura, toteż polecenie powinno być tutaj nieco bardziej doprecyzowane, żeby nie było niejasności co należy zrobić i zapewne tak by było gdyby analogiczne zadanie pojawiło się na "dzisiejszej" maturze.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W pp3) mamy tak na dobrą sprawę dużą dowolność działania - należy zauważyć, że faktycznie do punktów pomiarowych z pp2) można na różne sposoby dopasować proste - jedne będą bardziej nachylone do poziomu, a inne mniej. Należy arbitralnie wybrać jedną, która jest najbardziej i jedną, która jest najmniej nachylona i dla nich obliczyć wartość g. Wartość g można obliczyć wykorzystując fakt, że współczynnik kierunkowy prostej to tg(alfa), a ponadto wiemy, że okres drgań dla wahadła to T = 2*pi*pierw(l/g). Ponieważ zależność przedstawiona na wykresie to T^2 w funkcji l, to wzór na okres należy obustronnie podnieść do kwadratu i dostajemy: T^2 = 4*pi^2/g * l, więc współczynnikiem kierunkowym jest 4*pi^2/g. Obliczając z tego g dwukrotnie (dla obu dopasowań), dostaniemy jakąś maksymalną wartość i minimalną - na tej podstawie można okreslić niepewność bezwzględną, bo gmax = g + deltag oraz gmin = g - deltag.
Pp 4) jest raczej trochę dziwnie sformułowany i w takiej postaci zapewne nie pojawiłoby się to na naszej maturze, ale pozwolę sobie tutaj zwyczajnie skopiować uzasadnienie podane przez CKE: "Odszukaj w opisie doświadczenia ten etap, w którym polegamy wyłącznie na naszych zmysłach – nie posługujemy się żadnymi przyrządami pomiarowymi. Ma to miejsce wtedy, gdy dokonujemy oceny, czy okres drgań wahadła sprężynowego jest równy okresowi wahadła matematycznego. Ocena ta jest obarczona bardzo dużym błędem, a więc i długość nici l wahadła wyznaczona została niedokładnie."
5) Byłaby oczywiście różnica, bo g na Księżycu jest inne niż na Ziemi (w szczegółach będziemy to obliczali na zajęciach nr 20), więc taki sam okres drgań będzie miało na Księżycu wahadło wtedy, gdy jego długość będzie inna niż na Ziemi.