carmellio 55 wyśw.
29-01-2025 14:25
Zad 1, cz II, s. 96 podpunkt d)
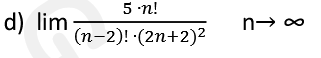
Cześć.
Nie potrafię zrozumieć procesu rozwiązania tej granicy.
Wiem, że robi się to tak:
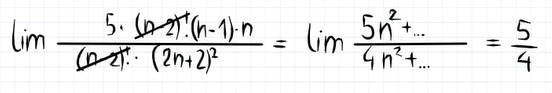
Ale nie rozumiem, dlaczego rozwijamy n! jako (n-2)!(n-1)n. Czy jest to uniwersalny wzór na (n!)? Nie widzę go w karcie wzorów.
Byłabym wdzięczna za wytłumaczenie.
matematyka rozszerzona granice silnia Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
MI3KO4AJ
29-01-2025 17:17
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jarosinski
02-02-2025 13:07
n! = 1 * 2 * 3 * ... * (n-2) * (n-1) * n, zatem n! = (n-2)! * (n-1) * n
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jakub
02-02-2025 15:58
tak jest to uniwerslany sposob zapisu, tutaj uzylismy (n-2)! zeby skrocic mianownik, ale jesli bylaby by potrzbea moglibysmy rownie dobrze zapisac to jako (n-4)!(n-3)(n-2)(n-1)n, tylko w wypadku tego zadania nic by nam to nie dalo
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
zobacz że np 7! to rozwinięcie 1*2*3*4*5*6*7. Zobacz że to samo co 5!(1*2*3*4*5) *6*7. Dlatego możemy to zapisać w taki sposób