ZZ.123

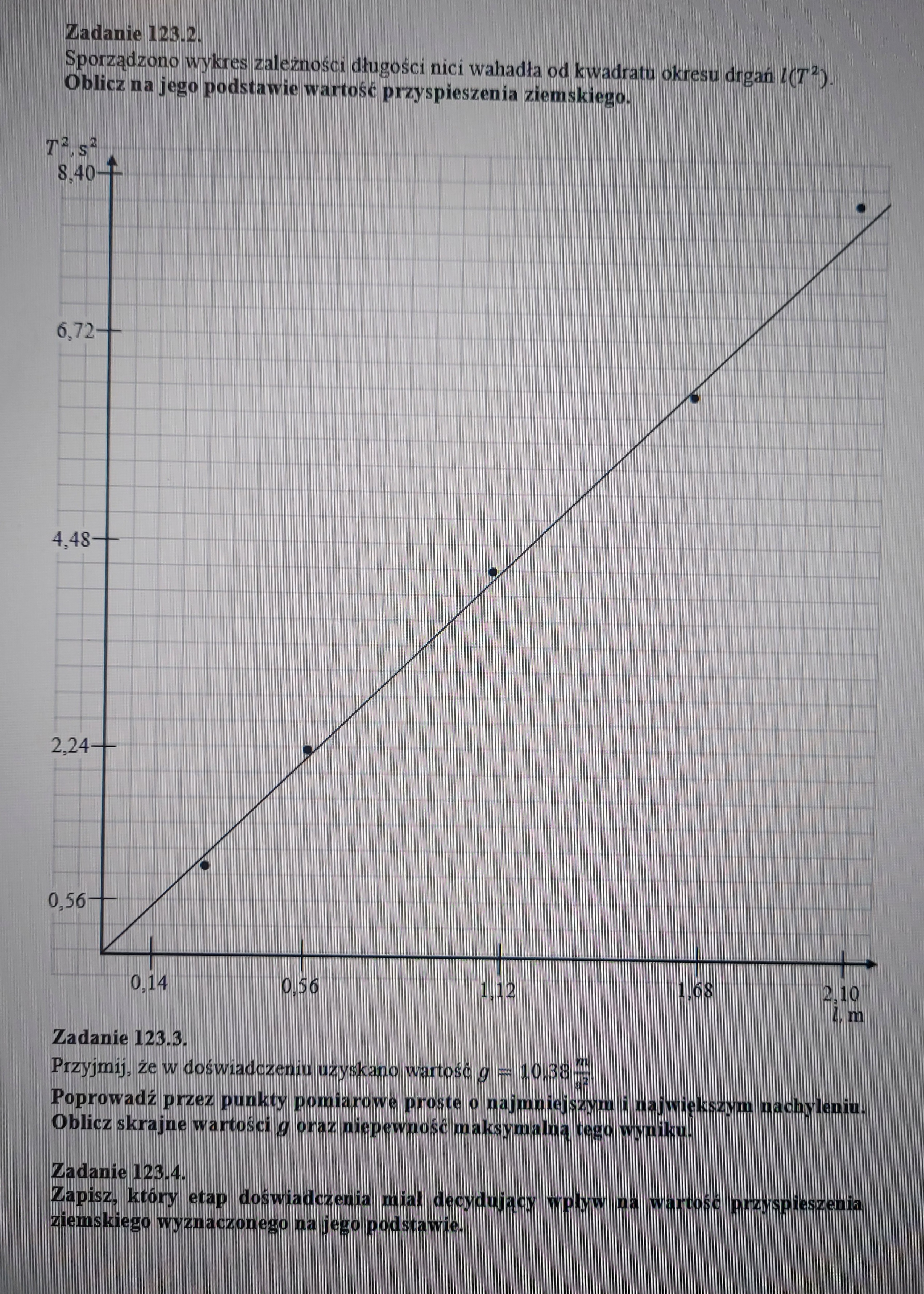


123.2.: Policzyłem g dla punktów początkowego i końcowego i wyszło mi dokładnie 9,81 a w odpowiedziach jest 10,38. Czy mój wynik byłby uznany?
123.3.: Tutaj także policzyłem dla innych punktów, więc wyniki są rozbieżne z odpowiedziami. Ale czy moje także byłyby uznane?
123.4.: Czy ta odpowiedź jest poprawna?
123.5.: Jak mam uzasadnić, że długości będą takie same? Napisać, że do pomiaru użyliśmy tej samej linijki czy coś tego typu?
Fizyka drgania Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
123.3.: To zakładam, że mam dobrze policzone gmax i gmin. A czy dobrze mam maksymalną niepewność? No bo ona może być równa (gmax-gmin)/2 lub gmax-g lub g-gmin gdzie g=10,38m/s^2 no i wybieram największą z tych wartości. Czy ten sposób jest poprawny?
123.5.: Czyli powinni dopisać jeszcze o równości okresów wahadeł na Ziemi i na Księżycu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3) Tak, to będzie ok.
5) Tak, to musi być doprecyzowane.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
2) Tak, będzie ok :)
3) tutaj zgodnie z treścią należałoby najpierw poprowadzić jakieś dwie proste - jedną o największym możliwym, a drugą o najmniejszym możliwym nachyleniu (robimy to arbitralnie, czyli "na oko") - i to dla nich obliczyć te wartości g. I powinny wyjść nam jakieś dwie wartości, z których jedna będzie większa niż 10,38, a druga mniejsza i będzie ok, nawet jeśli wyjdą one inne niż w odpowiedziach.
4) Tak jest.
5) Tutaj to pytanie jest standardowo jak na starsze matury niedoprecyzowane, bo autorom chodziło o to, że wyjdą im inne długości wahadeł, bo na Księżycu dla innych długości wahadeł okres zrównywałby się z okresem drgań masy na sprężynie.