ZZ.82

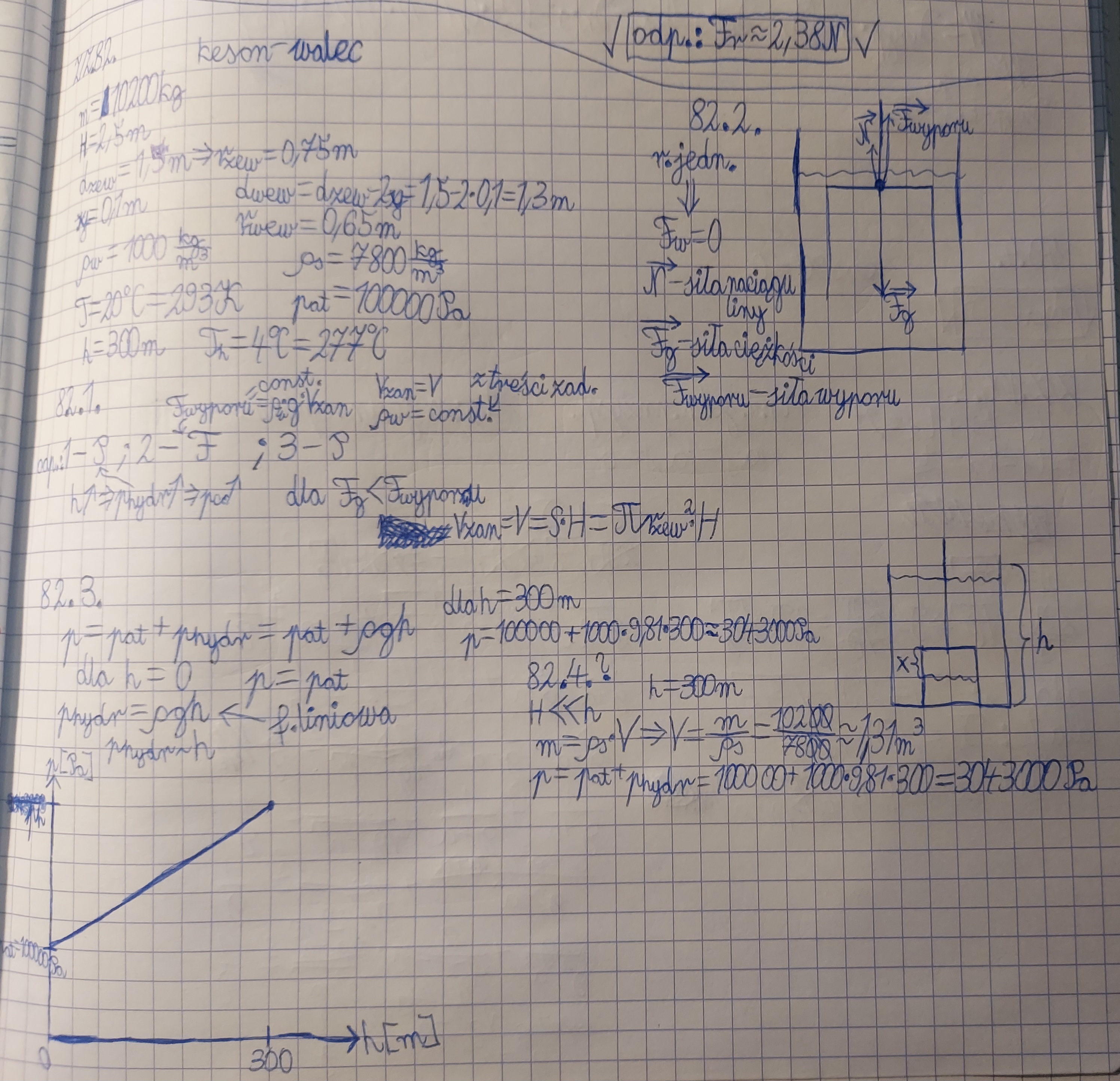
82.1.: Czy te moje "wytłumaczenia" są dobre?
82.2.: Czy wszystkie siły mogą być zaczepione w jednym punkcie?
82.3.: Czy na wykresie może nie być zachowana proporcja? Bo z tego co rozumiem to chodzi tylko o to, że jest to funkcja liniowa.
82.4.: Jak do tego podejść? Próbowałem z równaniem sił, ale wynik wyszedł jakieś 7,5m, więc to jest bez sensu, bo x musi być mniejszy od h=2,5m.
Fizyka hydrostatyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
82.3.: Chodzi mi o to, że dla h=0m p=1000hpa a dla h=300m p=30430hpa, no więc nie chcę robić rysunku na całą stronę, ale w sumie to chyba przekłada się na nachylenie prostej to mam nadzieję, że jest ok.
82.4.: Temperatura wody na głębokości 300m jest równa temperaturze powietrza? Ale x to przecież wysokość słupa powietrza.
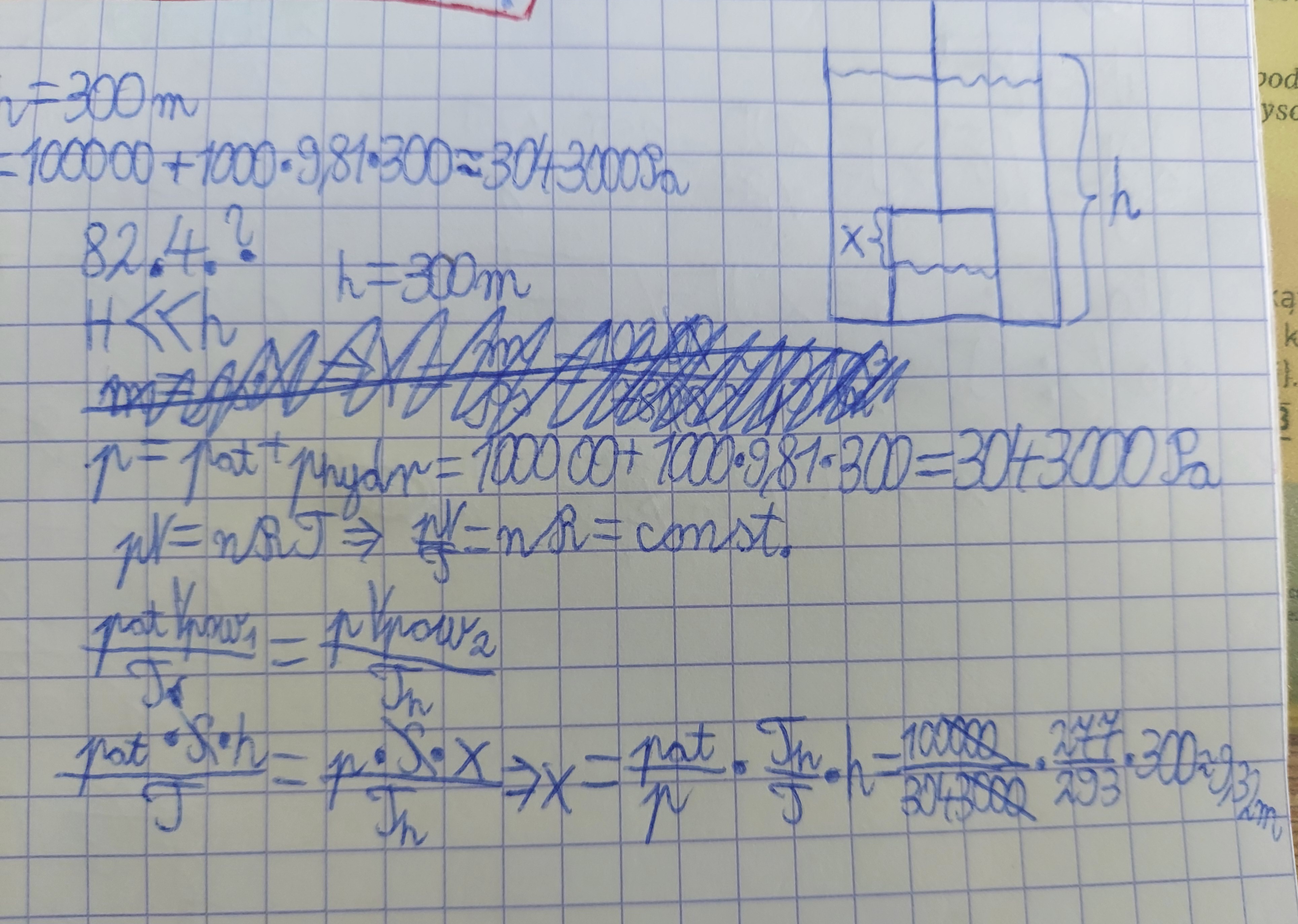
Gdzie mam błąd? Bo przecież x musi być mniejsze od 2,5m.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3) No to tak, nachylenie prostej można przyjąć sobie dowolne, bo osie nie muszą być wyskalowane tak samo :)
4) Nie no jest podane, że temperatura na dnie to 4 stopnie Celsjusza. Te wartości p, V i T są różne na powierzchni i na dnie. x to wysokość słupa powietrza, ale jak będziemy mieli x, to wystarczy odjąć od wysokości kesonu ten x i mamy już wysokość słupa wody w kesonie :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No ale podane jest, że temperatura wody przy dnie to 4 stopnie, więc zakładam, że powietrza jest tam taka sama tak?
A gdzie popełniłem błąd w obliczeniach?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, temperatura powietrza na dnie to 4 stopnie Celsjusza. Błąd jest taki, że przyjmujesz, że h = 300 m, ale przecież w tym równaniu stanu gazu doskonałego przyrównujemy do siebie powietrze w kesonie na powierzchni i przy dnie. Więc to h to jest po prostu wysokość kesonu, czyli 2,5 m. Jeśli wrzucisz tam takie własnie h, to bedzie ok.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A w sumie mam takie pytanie teoretyczne: jak to działa, że gdy zanurzymy całkowicie keson to w całej jego objętości nie będzie woda tylko część będzie zajmowało powietrze?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wynika to z tego, że z tym powietrzem coś się musi przecież stać, nie może ono po prostu "zniknąć" ;) więc zgodnie z równaniem Clapeyrona i prawem Pascala kompresuje się ono do mniejszej objętości (tym mniejszej im głębiej jesteśmy).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A istnieje jakaś graniczna wartość, od której powietrze całkowicie "znika" z kesonu? Bo wyobrażam sobie to tak, że mogłoby się tak stać i wtedy powstałyby pęcherzyki powietrza "wędrujące" w górę (przynajmniej tak mi się wydaje).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie - oczywiście można stamtąd powietrze "wyprowadzić", ale trzeba by to jakoś "sztucznie" zrobić, tak, żeby mogło dołem kesonu opuścić go. Natomiast oczywiście im głębiej będziemy schodzili, tym mniejsza będzie objętość tego powietrza w kesonie (aż granicznie będzie dążyła do zera).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A to doświadczenie da się zrobić samemu w domu? Bo próbowałem wkładać szklankę do garnka, ale nie widoczna jest różnica pomiędzy wodą a powietrzem w kolorystyce.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Oczywiście. Musisz tylko tak włożyć szklankę do wody, aby bąbelki powietrza nie uciekały na zewnątrz i wtedy powietrze zostaje w środku. A jeśli nie widzisz różnicy to lepiej użyć zamiast garnka jakiegoś mniejszego naczynia i wtedy wkładając do niego szklankę/kieliszek zauważyć będzie można wyraźnie podnoszenie się poziomu wody w naczyniu - to oznacza, że w środku szklanki zostało powietrza i jego objętość wypycha taką samą objętość wody w górę.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1) Siłą wyporu wręcz maleje, bo maleje objętość powietrza w kesonie, czyli Vzan robi się coraz mniejsze, to dlatego jest tam fałsz. reszta jest ok.
2) Tak, będzie ok.
3) Jeśli masz na myśli to czy może być różne nachylenie tej linii prostej to tak :)
4) Trzeba wykorzystać równanie Clapeyrona dla powietrza w kesonie. Czyli pV/T = const, a zatem pV/T na powierzchni jest równe pV/T na głębokości 300 m. Zauważmy, że na powierzchni mamy wszystkie te trzy parametry podane (V trzeba oczywiście obliczyć jako S*h, gdzie S to pole podstawy walca, którym jest keson, a h to jego wysokość). Z kolei na głębokości 300 m ciśnienie obliczymy wykorzystując prawo Pascala - ciśnienie wewnątrz kesonu (na granicy woda-powietrze) musi być takie jak wody na zewnątrz, a to jest suma ciśnienia hydrostatycznego i atmosferycznego. Temperaturę przy dnie mamy podaną, a V powietrza przy dnie to będzie S*x. Wyliczymy z równania stanu gazu doskonałego teraz x i mamy wysokość słupa wody.