kstrus 50 wyśw.
05-02-2025 09:08
ZZ.N.23
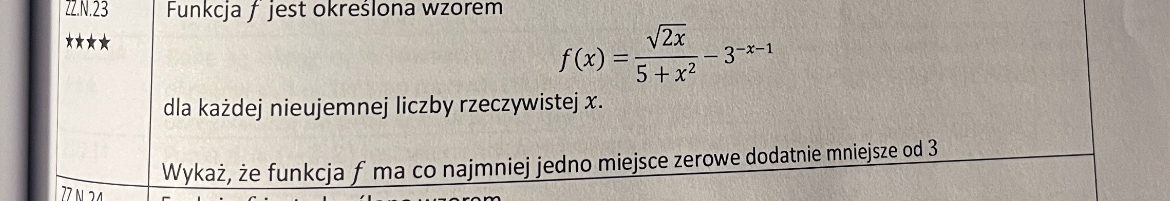
Czy w tym zadaniu wystarczy policzyć f(0), f(3) i wykorzystać twierdzenie Darboux w (0, 3) do wykazania prawdziwości tezy? Próbowałem liczyć pochodną ale tak średnio wyszło.
ZZ.N.23 różniczkowy Draboux Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
MI3KO4AJ
05-02-2025 10:00
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
kstrus
05-02-2025 12:14
To jak w takim razie wykazać ciągłość funkcji bez liczenia pochodnej?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
MI3KO4AJ
05-02-2025 12:34
pochodna nie ma nic do ciągłości funkcji. Funkcja jest nieciągła gdy coś wypada z dziedziny. Tutaj jest suma funkcji wymiernej i wykładniczej. Trzeba zbadać czy są to funkcje ciągłe (zobaczyć czy coś wypada z dziedziny)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak. Pamiętaj aby uwzględnić ciągłość funkcji