ZZ.122

mam kilka pytań do zadnia :)
pp2) z ciekawości- dlaczego nie mogłoby być tutaj odp 1,B ?
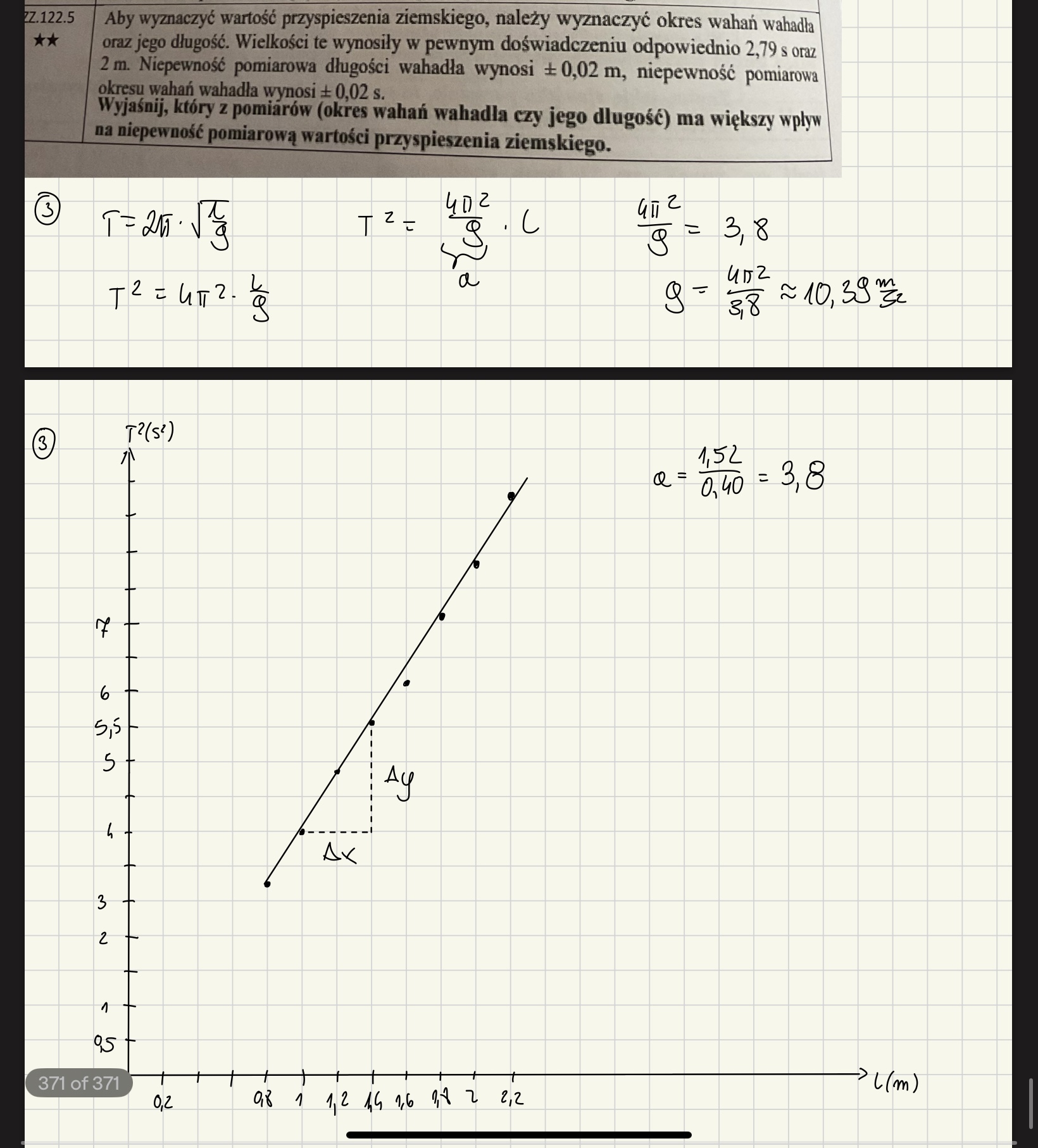
pp3) czy tak też jest okej? w odp widziałam, że biorą jakiś jeden pkt z wykresu i go podstawiają do wzoru na g (przekształconego z wzoru na T^2) i wynik wychodzi trochę inny
pp5) potrzebuje pomocy z tym pp. czytałam już inne wyjaśnienie na forum, ale niestety nadal nie do końca wiem jak to zrobić
wahadło niepewności Dodaj post do ulubionych Poproś o pomoc
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale mimo to metoda podana przez CKE jest błędna prawda? Bo oni podnoszą niepewność okresu do kwadratu.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Podana przez nich metoda jest niepoprawna dlatego, że oni w ogóle sugerują tam porównanie l + deltal oraz T + deltaT, co jest bez sensu ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
PP 2) to zdanie B jest oczywiście prawdziwe, natomiast zdecydowanie najlepszym uzasadnieniem jest zdanie C. Choć oczywiście pośrednio rzecz przytoczona w zdaniu B też przekładałaby się na fakt, że użyty wzór nie podawałby w takiej sytuacji dokładnych wyników.
Pp 3) - tak, jest to jak najbardziej ok :) a to, że wynik wychodzi trochę inny to normalna sprawa w przypadku obliczania jakiejś wielkości na podstawie odczytu z wykresu.
Pp 5) Aby formalnie to określić to należy sprawdzić, która z tych wielkości cechuje się większą niepewnością względną (i to jest ogólny przepis na sprawdzanie tego, która z niepewności ma większy wkład w niepewność końcowego wyniku - trzeba porównać niepewności względne wyznaczenia danych wielkości). Niepewność względna danej wielkości to jej niepewność bezwzględna podzielona przez wartość samej tej wielkości. Więc w tym przypadku niepewność względna pomiaru długości jest większa niż czasu (0,02/2 > 0,02/2,79), ale tu sytuacja jest delikatnie inna, ponieważ jeśli spojrzymy na wzór na przyspieszenie ziemskie, to widzimy tam g = 4*pi^2*l/T^2. T jest podniesione do kwadratu, a l nie. Okazuje się, że w takiej sytuacji w przypadku tej wielkości, która jest podniesiona do kwadratu tę jej niepewność względną trzeba jeszcze przemnożyć przez 2 (wynika to z tzw. prawa przenoszenia niepewności, które wiąże się z liczeniem pochodnych - nie będzie tego na naszej maturze) i dlatego akurat niepewność czasu ma tutaj jednak większy wkład w całkowitą niepewność wyznaczenia g. Natomiast z uwagi na fakt, że to formalnie jest ponadprogramowe, to w tej sytuacji musieliby na "dzisiejszej" maturze wyraźnie powiedzieć, że tam musi się pojawić to przemnożenie przez dwójkę (natomiast wszystko wskazuje na to, że samo porównywanie niepewności względnych jest czymś co powinniśmy umieć).