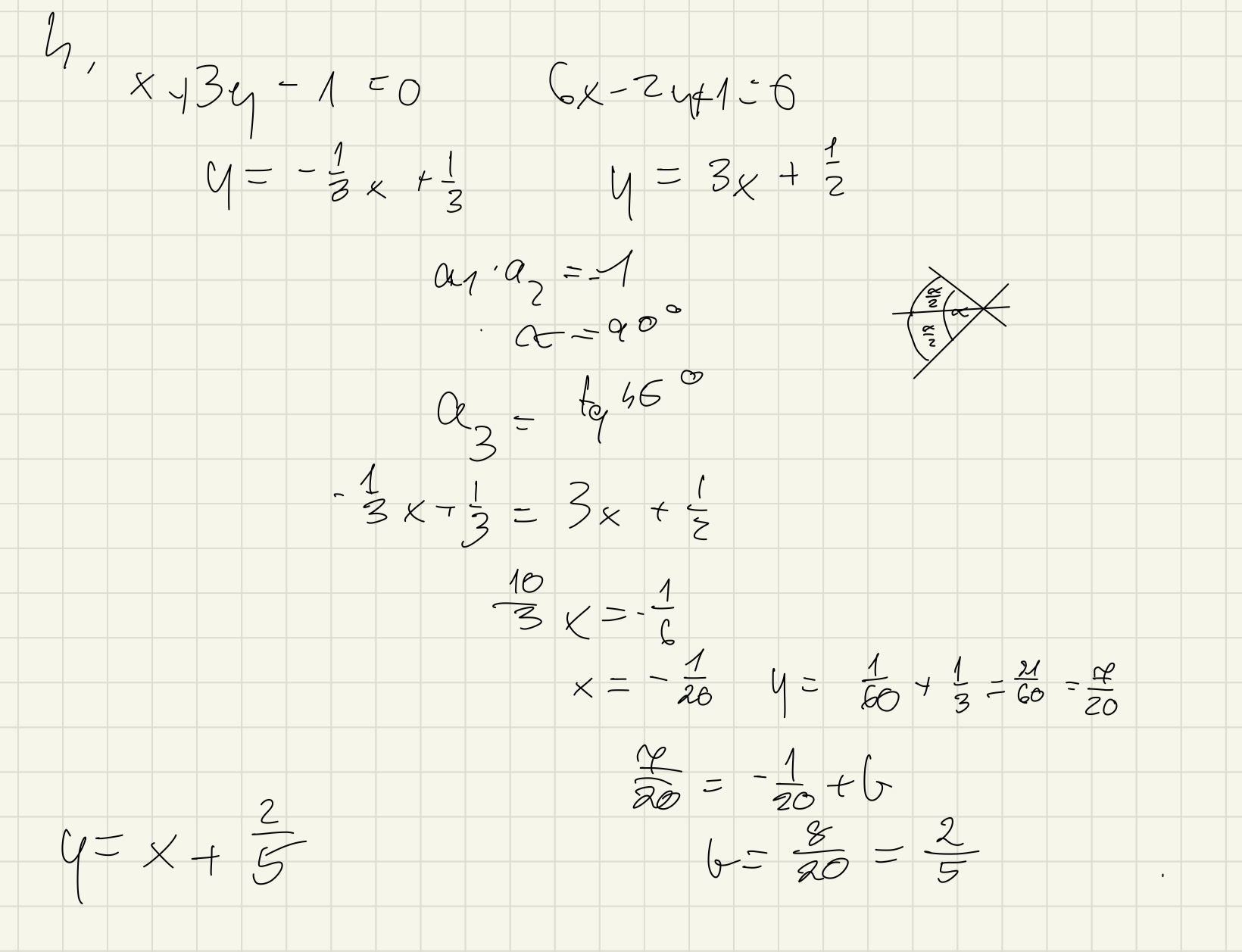Zad 4
Znajdź równanie dwusiecznej kąta, przecięcia się dwóch prostych x+3y-1=0 oraz 6x-2y+1=0
Dlaczego w tym zadaniu nie można wykazać że te dwie prosta są prostopadle do siebie i z tego wyprowadzić a dwusciecznej
Zbiór zadań Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W sumie racja, robiłeś tym sposób i wynik wyszedł ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No właśnie nie wyszedł taki jaki powinien
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
mozesz tutaj podeslac zdjecie twojego rozwiazania
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ja też tak na początku zrobiłam, ale potem narysowałam te proste w układzie współrzędnych. Moim zdaniem nie można skorzystać z tego że tg alfa = a, ponieważ prosta która oznacza dwusieczna nie jest nachylona do osi x pod kątem 45 stopni. Jest nachylona pod tym kątem jedynie do jednej z prostych, ale sam widzisz że na rysunku są dwie opcje tej dwusiecznej i każda z nich jest inaczej nachylona do osi ox i ma więcej stopni niż 45. Więc nie możemy zastosowac tego, że tg alfa = a , bo alfa to kąt nachylony względem osi x. 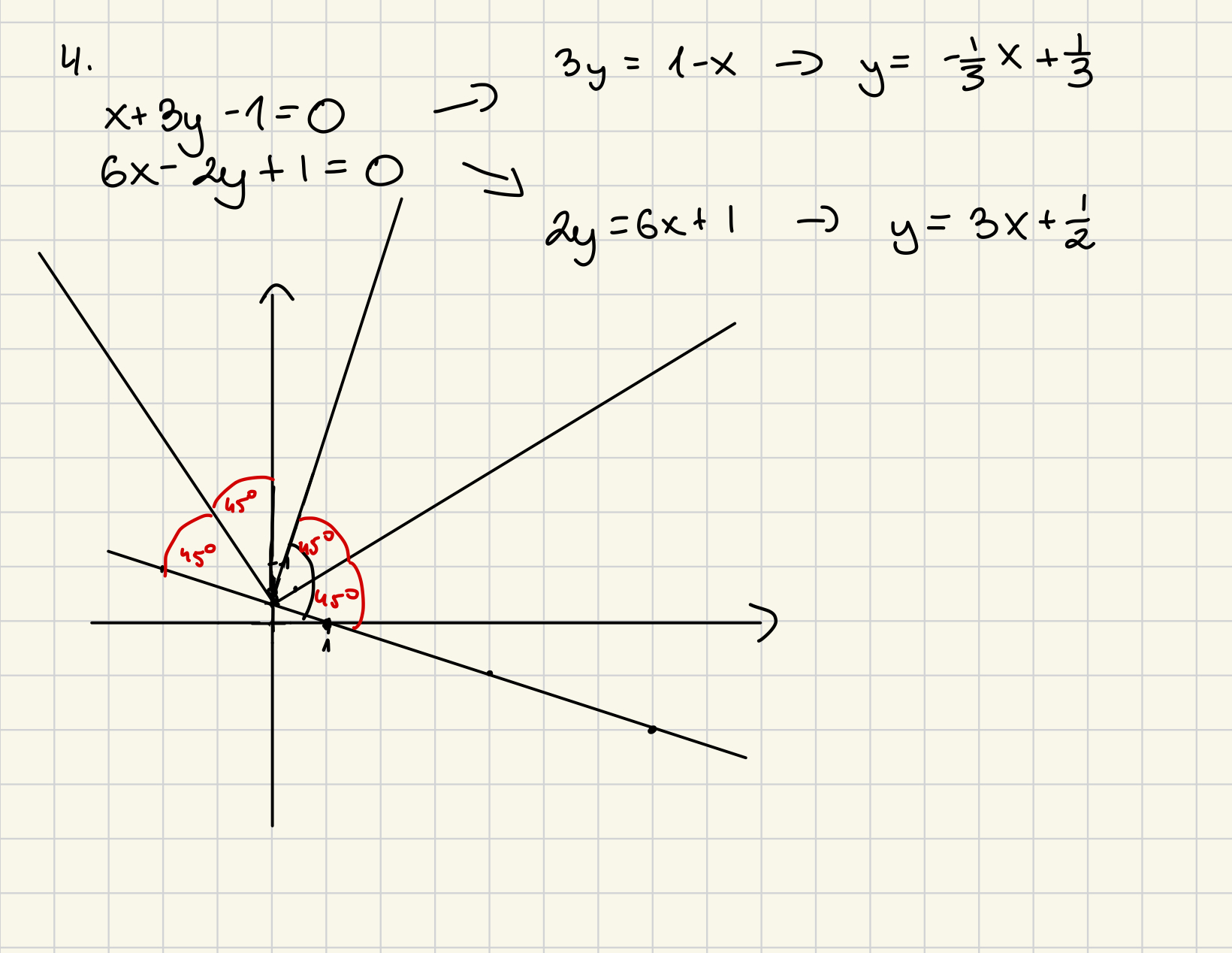
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Korekta: kąt dwusiecznej do osi x nawet nie jest nachylony jak powinien byc, bo zaczyna się gdzieś na osi y, a nie w punkcie 0,0
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
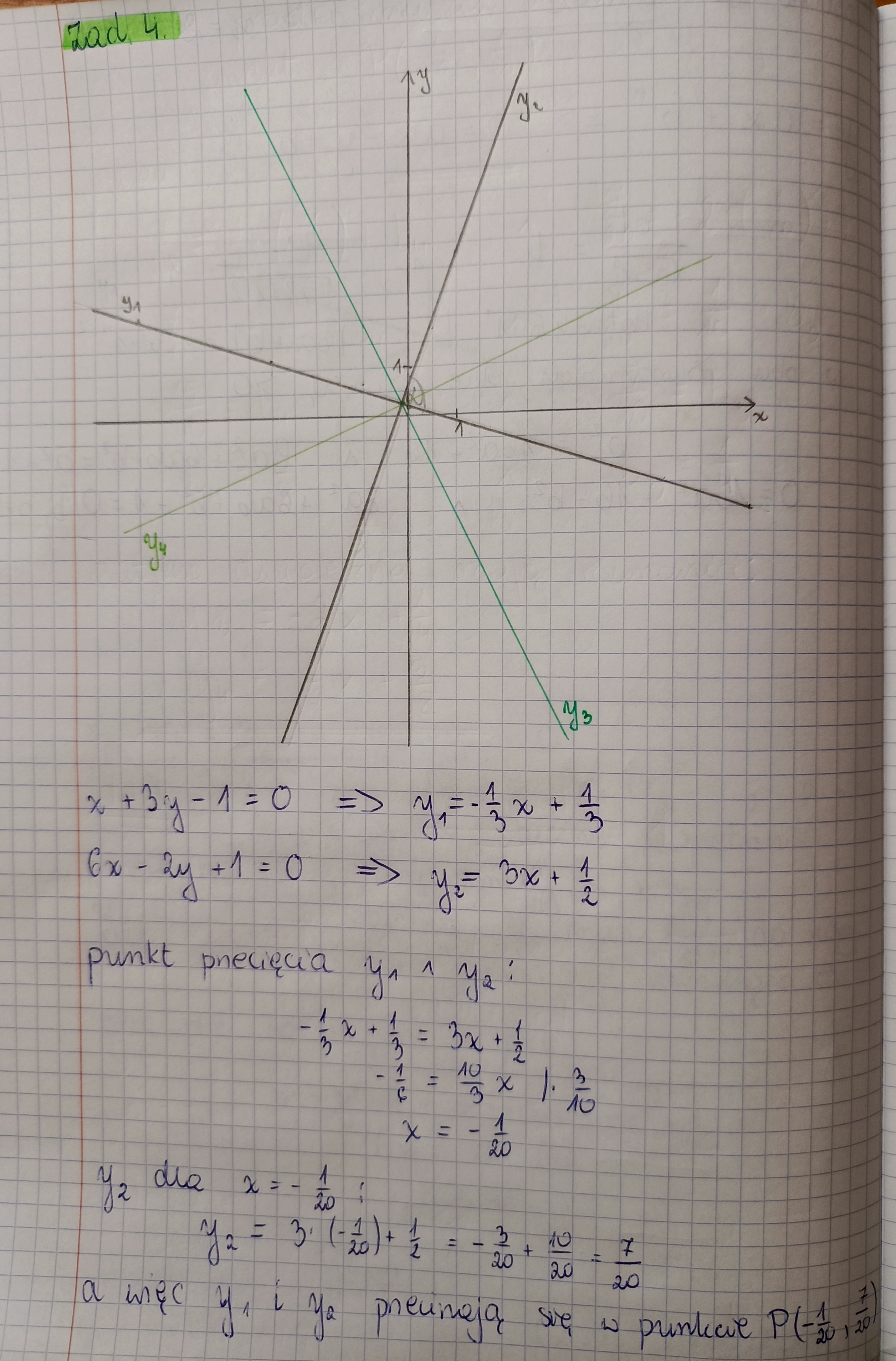


Ja zadanie zrobiłam wykorzystując nachylenie prostych względem siebie, kąt 90° i jego połowę oraz wzór na tgα uwzględniający współczynniki a₁ i a₂, i wynik wychodzi poprawny
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych