praca domowa 19; zadanie 5

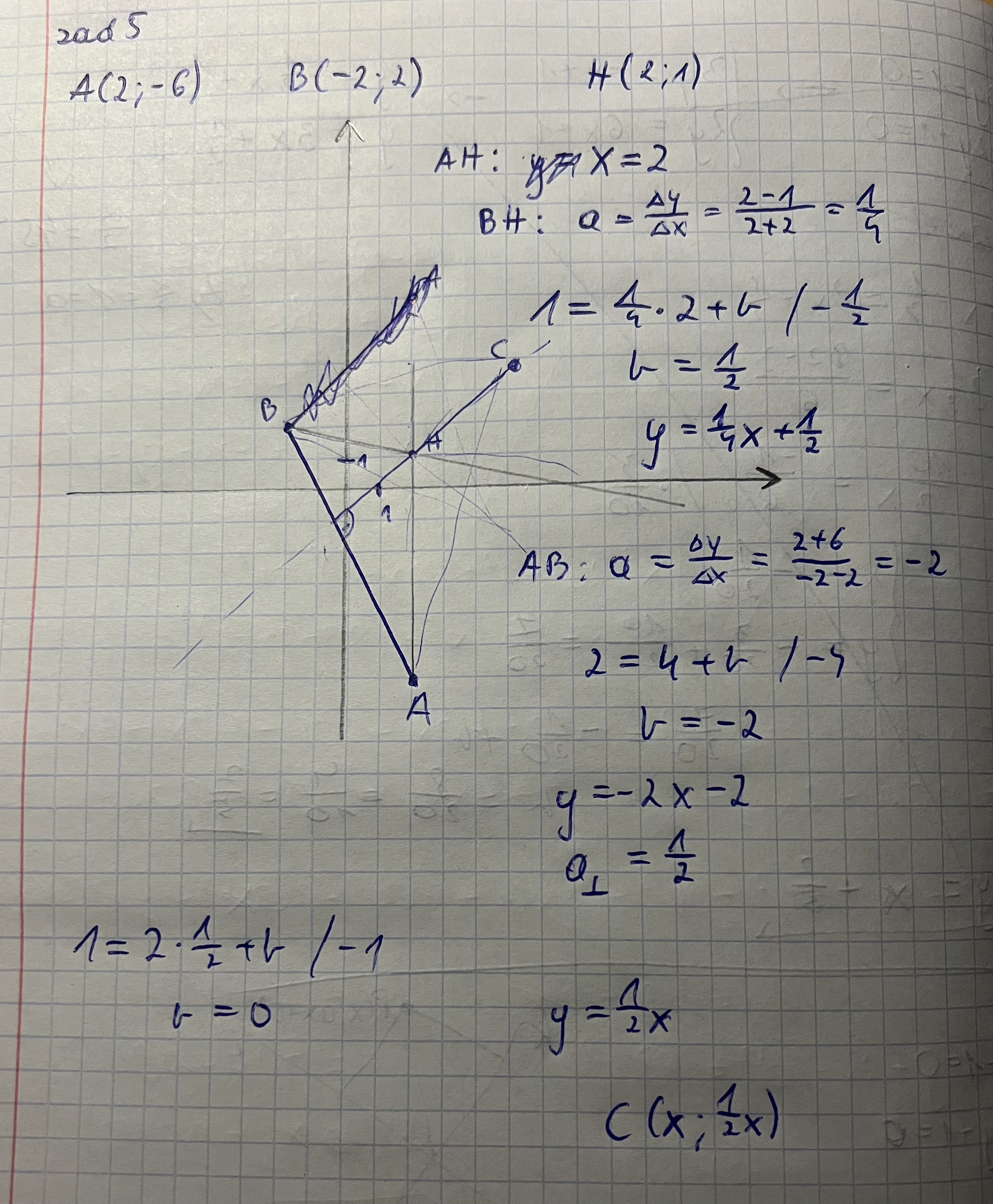
 Dlaczego punkt C jest przecięciem prostej y=2 z y=1/2x? Dlaczego nie może być dowolny?
Dlaczego punkt C jest przecięciem prostej y=2 z y=1/2x? Dlaczego nie może być dowolny?
matematyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
też się na tym zastanawiałem , wydaje mi się, że chodzi o to, że punkt H jest punktem przecięcia wysokości poprowadzonej z punktu A i wysokości poprowadzonej z punktu C. Dlatego punkt C nie może być dowolnym punktem na prostej, bo kąt padania wysokości na bok AC musi być równy 90 stopni. Jednakże nie jestem tego pewny.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W tym zadaniu ważne jest to, że wysokość w trójkącie opuszczona na dany bok, jest do niego prostopadła.
Wysokość opuszczona z punktu A przechodzi, zgodnie z treścią, przez punkt H. Na podstawie współrzędnych tych punktów widzimy, że jest ona prostopadła do osi OX i ma równanie x=2. Zatem skoro prosta zawierająca bok BC jest do wysokości opuszczonej z punktu A prostopadła, to musi być równoległa do osi OX (czyli mieć postać y=n, gdzie n to stała liczba). Prosta, na której leży bok BC, przechodzi przez punkt C oraz przez punkt B, którego współrzędna y = 2. Wynika z tego, że bok BC leży na prostej o równaniu y=2.
Wysokość opuszczona z punktu C przechodzi przez punkt H oraz jest prostopadła do boku AB, a więc (wyznaczając wcześniej równanie prostej, na której leży bok AB, znając współrzędne punktu A i B) możemy wyznaczyć równanie prostej, na której leży wysokość opuszczona z wierzchołka C (jest to prosta o równaniu y = 1/2 x). Skoro na tej prostej leży wysokość opuszczona z wierzchołka C, to ta prosta musi przechodzić przez punkt C.
Zatem punkt C leży na prostej, na której znajduje się bok BC oraz na prostej, na której znajduje się wysokość opuszczona z wierzchołka C. Proste te przecinają się raz (co wynika z ich równań). A więc punkt C musi leżeć na przecięciu tych prostych.