2008.5
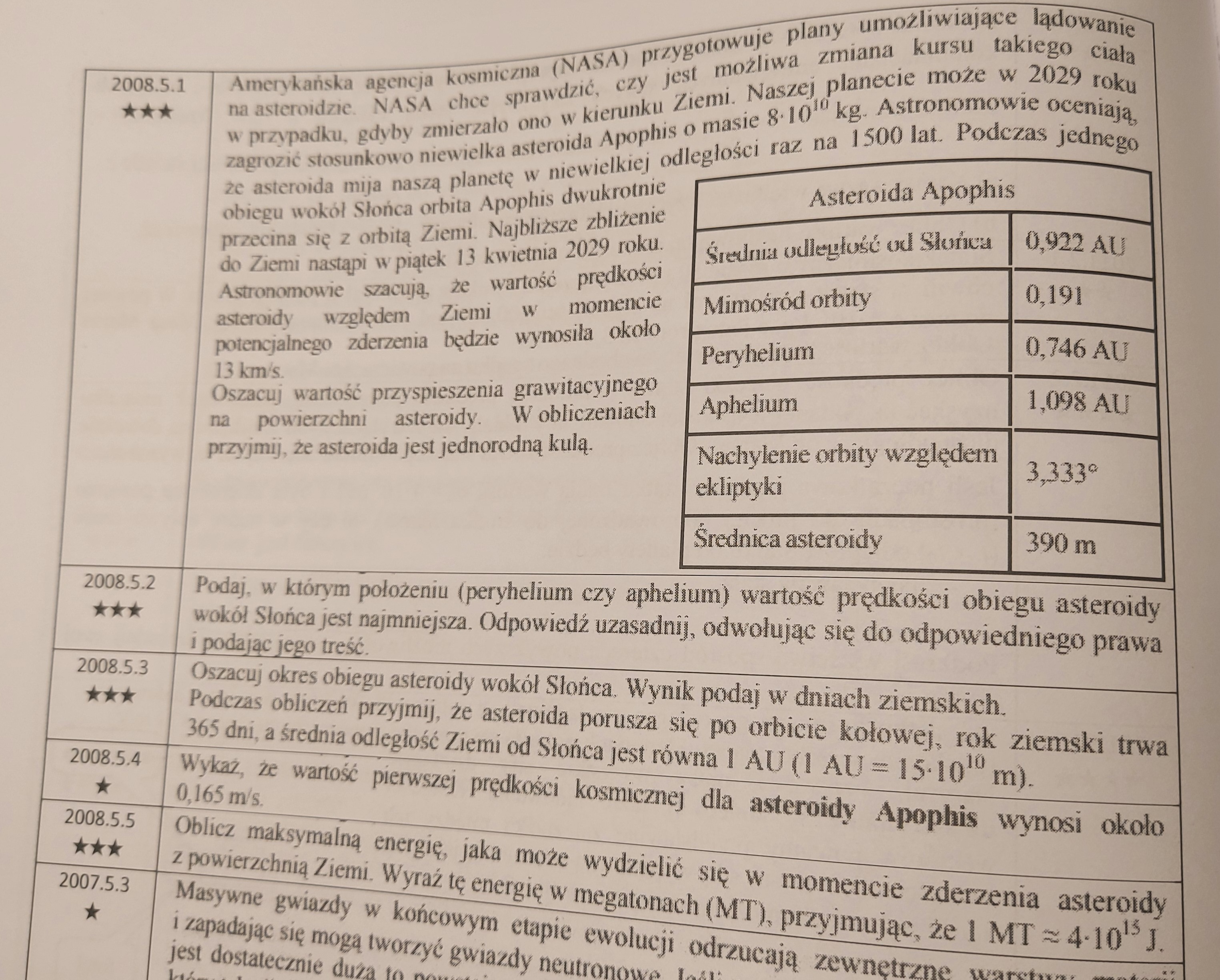


5.2.: Czy takie uzasadnienie byłoby prawidłowe?
5.5.: Może trochę uprzedzę temat, bo energii w grawitacji jeszcze nie było na kursie, ale chciałem spróbować to zrobić i nie wiem dlaczego nie bierze się pod uwagę energii potencjalnej.
Fizyka grawitacja Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
5.5.: No ale jak tak patrzę to pomijając energię potencjalną to wzór powinien wyjść taki sam tylko bez minusa. Ekin=GMz*Msat/2Rz^2
Im w odpowiedziach wychodzi, że Vor=13km/s a u mnie Vor=V1=7,9km/s
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale tak obliczona energia kinetyczna to jest energia kinetyczna dla ciała poruszającego się wokół innego ciała po orbicie kołowej o promieniu Rz pod wpływem siły grawitacji. A tutaj asteroida nie porusza się w ten sposób ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A bo my mamy jeszcze prędkość (tego nie zauważyłem). To po prostu mV^2/2? Gdyby nie było danej prędkości to da się to jeszcze jakoś inaczej obliczyć?
W jaki sposób porusza się zatem ta asteroida? Bo trochę tego nie rozumiem.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, po prostu mv^2/2. Bez tej prędkości nie mamy jak tego tutaj policzyć. Jak dokładnie porusza się asteroida to tego nie wiemy, ale zapewne jest to jakaś krzywa, której tor akurat przetnie się z torem ruchu Ziemi.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
2: Powinno być raczej pole zakreślone przez promień wodzący ciała, a nie przez samo ciało (ale może by to przepuścili). A tak to jest w porządku.
5: Tu znów wchodzi w grę trochę zbyt słabe doprecyzowanie (a w zasadzie żadne) jak takie zderzenie miałoby wyglądać. Bo oni tak naprawdę założyli (całkiem sensownie), że tuż przed zderzeniem asteroida znajduje się w odległości w przybliżeniu równej Rz od środka Ziemi (promień asteroidy możemy pominąć bo jest zaniedbywalnie mały), a po zderzeniu ta asteroida dalej znajduje się w tej samej odległości (bo zatrzymała się w momencie uderzenia w powierzchnię Ziemi). Czyli w wyniku zderzenia energia potencjalna układu Ziemia-asteroida nie uległa zmianie, stąd wyzwolona podczas uderzenia energia wzięła się całkowicie z energii kinetycznej asteroidy.