Przemiana Izoaryczna
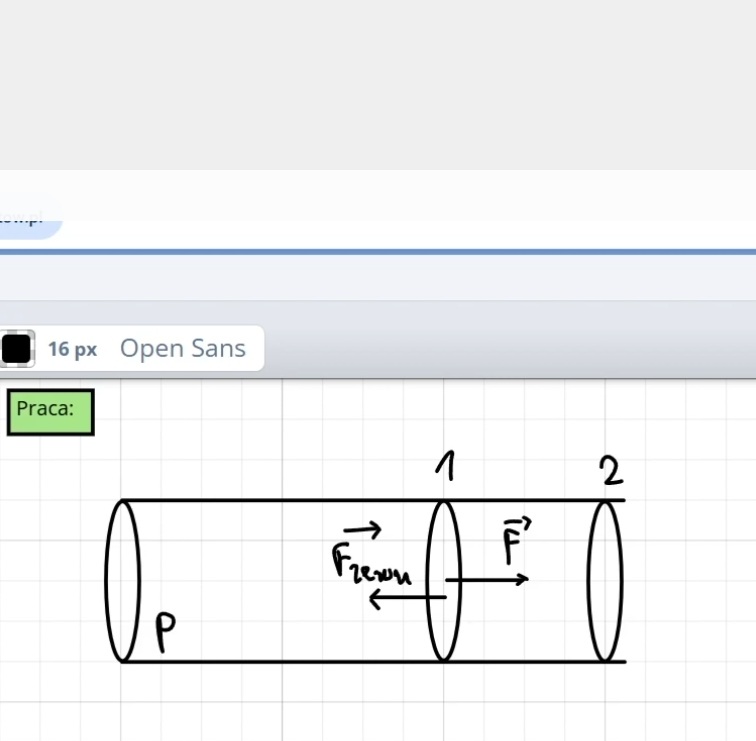
Czemu to jest przemiana izobaryczna? Jeśli objętość się zmienia i raz cząstki gazu ściskamy a raz rozprezamy czy to nie wpływa na ich ciśnienie? Dlaczego wiemy też temperatura nie jest stała?
#Fizyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tzn. wprowadzając przemianę izobaryczną na zajęciach my rysując sobie taki cylinder założyliśmy odgórnie, że jest to przemiana izobaryczna. Rysunek miał za zadanie zobrazować sytuację tak by łatwo było zobaczyć, że w określony sposób można zapisać pracę w przemianie izobarycznej.
Natomiast w praktyce i w zadaniach maturalnych musimy wiedzieć, że gdy mamy przemianę, w której gaz zamknięty jest ruchomym tłokiem, który może się swobodnie przemieszczać i dostarczamy lub odbieramy ciepło od ciała nie działając właśnie na ten tłok żadną dodatkową zewnętrzną siłą, to taka przemiana będzie właśnie przemianą izobaryczną. A to wynika z faktu, że skoro tłok może się swobodnie przemieszczać, to znaczy, że na skutek np. dostarczenia ciepła do gazu w cylindrze, jego ciśnienie będzie "próbowało" się zwiększyć, co delikatnie zwiększy siłę parcia gazu na tłok - ten w wyniku nierównowagi sił przesunie się zatem nieco do momentu aż siły na niego działające się zrównoważą i wtedy mamy już brak jego przesuwania - siła parcia gazu równoważy się z siłą parcia pochodzącą od gazu na zewnątrz (np. powietrza atmosferycznego), a zatem oznacza to, że ostatecznie ciśnienie się nie zmieniło - ten proces w przypadku niezbyt szybkiego ogrzewania zachodzi płynnie, wobec czego taką przemianę faktycznie możemy nazwać izobaryczną. A to, że wzrasta wtedy również temperatura (przy opisywanym ogrzewaniu) wynika chociażby wprost z równania Clapeyrona, skoro pV= nRT i p pozostaje stałe a V rośnie, to po prawej stronie równania T musi wzrosnąć.