2022.7

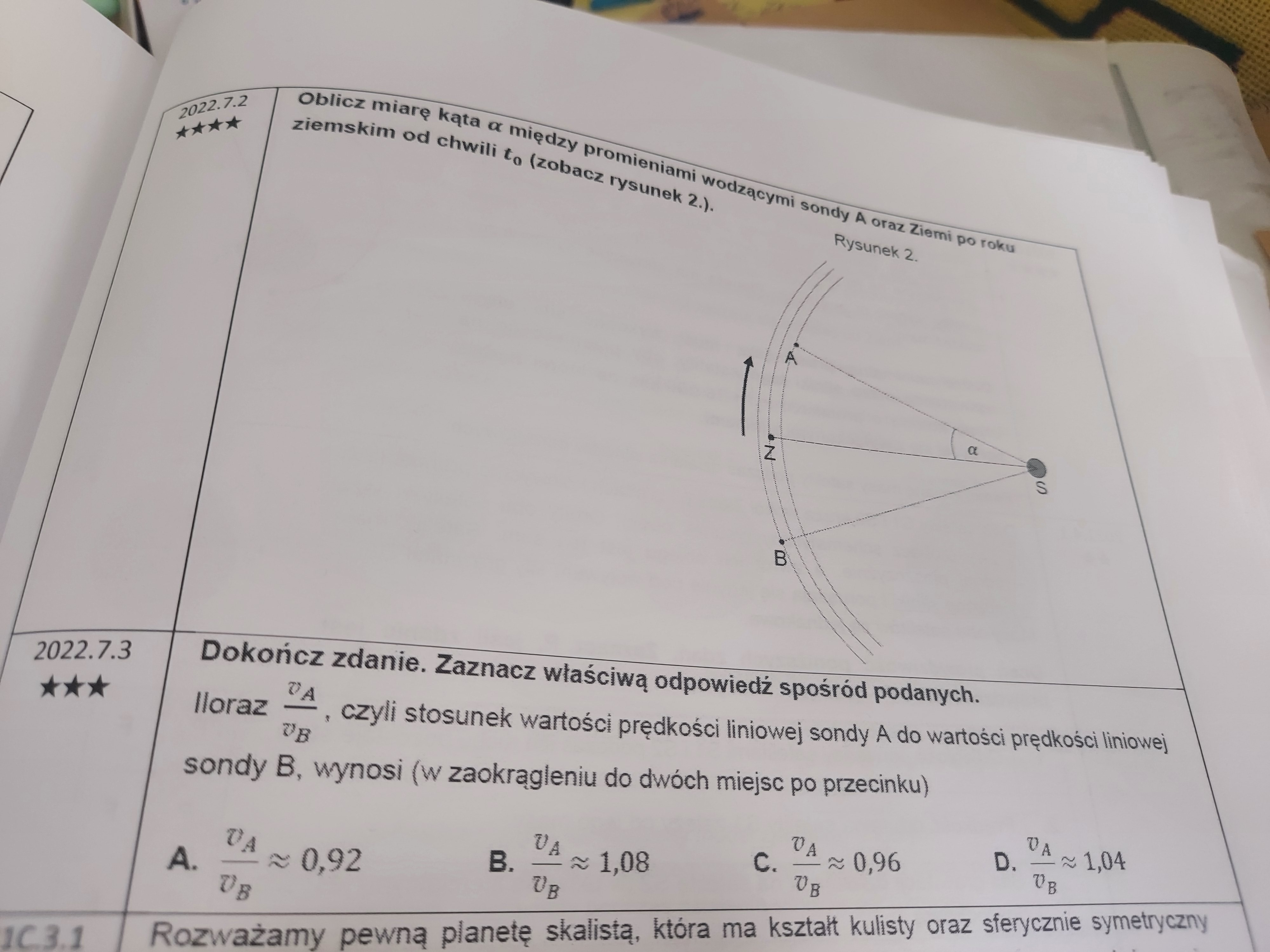

7.2.: Czy to rozumowanie jest prawidłowe czy trzeba tu coś jeszcze dopisać? I czy zostawienie tego wyniku bez zamiany na radiany też jest ok?
7.3.: Jak dojść do poprawnego wyniku? Myślałem, że chodzi o 2 PK, ale wtedy wychodzi mi odpowiedź B.
Fizyka grawitacja Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A dlaczego nie można z 2PK w 7.3.?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Hmm, tylko nie za bardzo widzę jak tu wykorzystać II PK? Ono działa dla jednego konkretnego satelity w ruchu po orbicie eliptycznej. A tu mamy dwa różne ciała w ruchu po orbicie kołowej.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A może to w sumie być dlatego, że satelity są na różnych orbitach. Gdyby różne satelity były na tej samej orbicie/elipsie to zadziałałoby 2 PK?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Próbowałem zrobić podpunkt 7.2 jeszcze raz, aby przypomnieć sobie jak robiło się to zadanie i nie wiem gdzie mam błąd :/
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie możesz tutaj użyć sobie takiej proporcji dla dwóch różnych ciał - Ziemi i sondy A. Mógłbyś ją użyć dla jednego ciała - np. dla Ziemi albo dla sondy.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chodzi o tę druga proporcję z tymi kątami. Przecież te ciała poruszają się po różnych orbitach. Więc jeśli np. sonda A pokona np. 2 razy większą drogę niż Ziemia, to nie oznacza wcale, że zakreśli dwa razy większy kąt. A Twoja proporcja to właśnie sugeruje.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A mógłby Pan pokazać to na przykładzie z liczbami? Chyba rozumiem ideę, ale chciałbym się upewnić.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Hmm, możesz Ty spróbować to policzyć, wtedy sam najlepiej to zobaczysz :D wystarczy tak naprawdę jedno obliczenie. Przyjmijmy, że Ziemia wykona połowę swojego obiegu, czyli pi*rz - wtedy zakreśli ona kąt 180 stopni. Niech teraz sonda A pokona dwa razy większą drogę, czyli 2*pi*rz - zgodnie z tamtą Twoją propozycją proporcji powinno wyjść, że wykona ona wtedy jeden pełny obrót, czyli zakreśli 360 stopni. Ale widzimy od razu nawet bez liczenia, że tak nie jest, bo żeby zakreślić 360 stopni, to sonda A musiałaby pokonać drogę 2*pi*ra, a nie 2*pi*rz.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A faktycznie już rozumiem. Czyli zawsze w sprawach tego typu jak te obrotowe trzeba się "trzymać" obliczeń co do jednego konkretnego ciała, bo inaczej wychodzi coś nieprawdziwego. Dziękuję :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
7.2: Jest ok.
7.3: Trzeba wykorzystać wzór na prędkość satelity w ruchu po orbicie kołowej, czyli v = pierw(GM/r)