2018.10

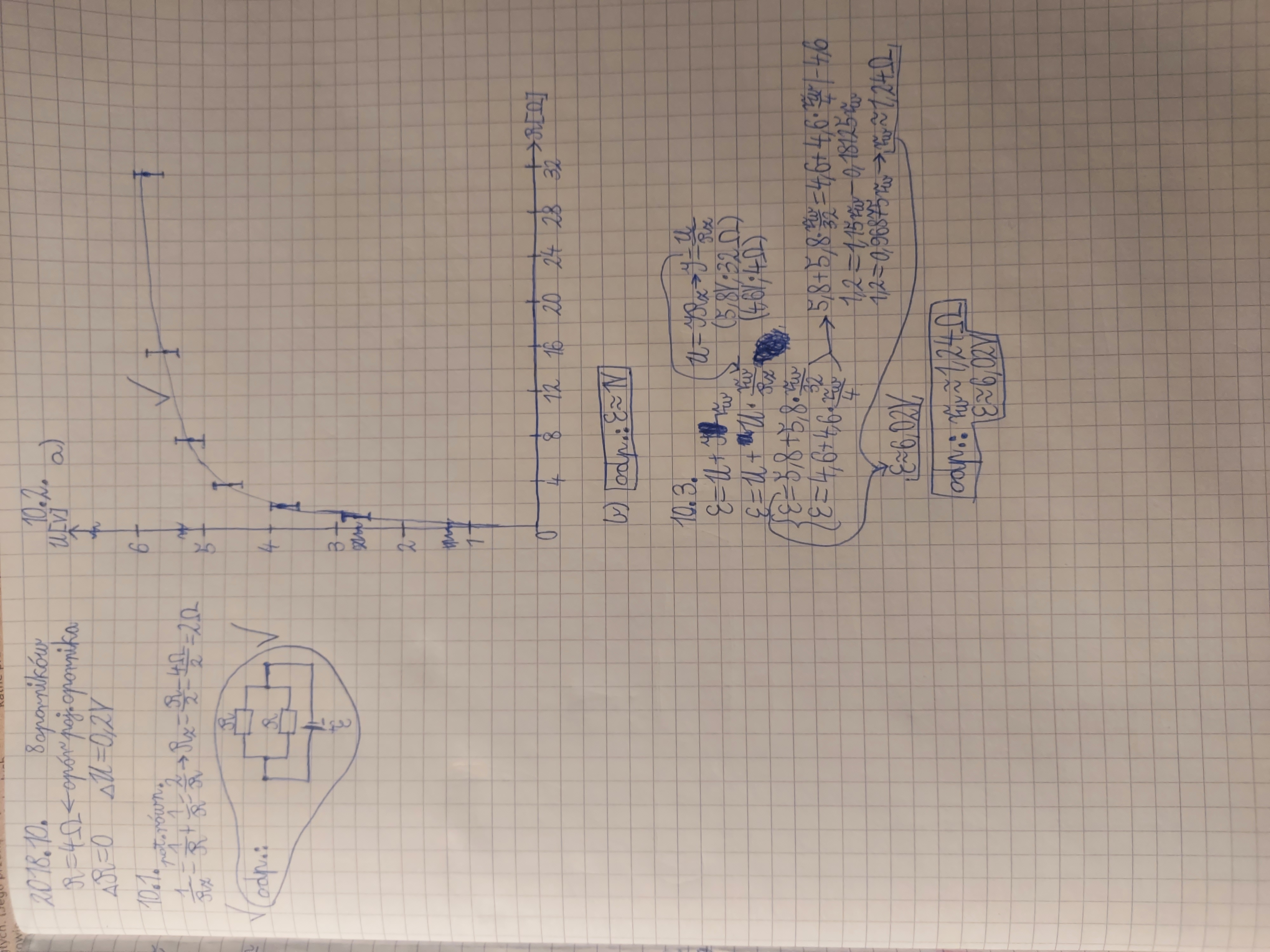
10.2.: a) Czy trzeba pisać, że ta krzywa to hiperbola? Jeśli tak to skąd to wiemy? b) Czy SEM to nie jest napięcie dla R=0? Bo zawsze tak robiliśmy z tego co pamiętam a tutaj tak nie jest.
10.3.: Czy takie wyniki byłyby uznane?
Fizyka prąd stały Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
10.2.: a) Wychodzi U=epsilon-I*rw? I to świadczyłoby o tej "hiperboliczności"?
b) To niezbyt rozumiem na jakiej podstawie mam odczytać, że epsilon=6V.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
U = E - I*rw, ale jednocześnie U = I*R. Więc mamy I*R = E - I*rw, stąd dostajemy I = E/(R+rw). Wrzucając to do pierwotnego wzoru dostajemy U = E - E*rw/(R + rw). Widzimy zatem, że jest to hiperbola (z minusem) przesunięta o wartość E w górę.
b) Zgodnie z treścią należy to odczytać z wykresu, a nie obliczać w żaden sposób. A widzimy, że zgodnie z wykresem krzywa, którą otrzymujemy zaczyna się wypłaszczać, a formalnie możemy powiedzieć, że posiada ona asymptotę poziomą - w nieskończoności wartości tej funkcji będą zbliżać się do właśnie 6 V (to, że jest tu asymptota pozioma nie powinno nas zresztą dziwić jeśli wiemy, że faktycznie jest tutaj hiperbola).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
b) Czyli my uznajemy, że opór SEM jest nieskończony? Jeśli tak to nie wiem dlaczego.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie, R to nie opór źródła napięcia, tylko zewnętrzny opór, który do źródła napięcia dołączamy. A wiemy z definicji SEM, że jest to napięcie na biegunach otwartego źródła. A otwarte źródło to takie, do którego nic nie jest podłączone, co jest tożsame z powiedzeniem, że podłączamy do niego nieskończenie wielki opór. A zatem idąc z R do nieskończoności faktycznie doprowadzamy do tego, że mierzone napięcie to jest właśnie SEM (zgodnie zresztą ze wzorem, który wyprowadziłem w poprzednim komentarzu - zauważ, że jak do niego wstawisz nieskończoną wartość R, to otrzymasz U = E).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli gdyby to był wykres epsilon(R) zamiast U(R) to epsilon byłoby odczytywane dla zerowego oporu? To jest odnośnie do: "b) SEM to napięcie dla R = 0, ale mierzone na źródle napięcia. Tu mierzymy napięcie na oporniku."
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ups, popełniłem wcześniej pomyłkę, chyba nie skupiłem się tak jak trzeba - przepraszam. Oczywiście SEM to nie jest napięcie dla R = 0, tylko dla R dążącego do nieskończoności. Tamto zdanie było zwyczajnie nieprawdziwe. Łatwo się tu nabrać, bo SEM to napięcie mierzonego gdy nie ma oporu zewnętrznego, ale to nie oznacza, że ten opór jest zerowy, ale właśnie, że opór dąży do nieskończoności. Celem zachowania przejrzystości również dla ew. innych osób czytających ten temat usuwam tamto błędne zdanie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale właśnie tak ogólnie wydaje mi się, że często SEM odczytywaliśmy z wykresu dla R=0. Czy tam była o czymś innym mowa?
"SEM to napięcie mierzonego gdy nie ma oporu zewnętrznego, ale to nie oznacza, że ten opór jest zerowy, ale właśnie, że opór dąży do nieskończoności."
Czy jest jakieś proste wytłumaczenie czemu tak się dzieje?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie przypominam sobie byśmy kiedykolwiek odczytywali SEM dla R = 0.
A wytłumaczenie jest takie, że jeśli mamy otwarte ogniwo, to znaczy, że nic do niego nie jest podłączone, więc można to potraktować tak, jakby między biegunami była próżnia (albo w dobry przybliżeniu powietrze). A próżnia charakteryzuje się bardzo wysokim oporem elektrycznym (w idealnym przypadku dążącym do nieskończoności).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
10.2 a) Nie trzeba tego pisać. Można to zauważyć zwyczajnie z II prawa Kirchhoffa wyprowadzając wzór na zależność U(R) w tym przypadku. Ale nie ma takiej konieczności.
b) SEM to napięcie nie dla R = 0, tylko dla R dążącego do nieskończoności.
10.3) Tak.