Wzór fizyczny

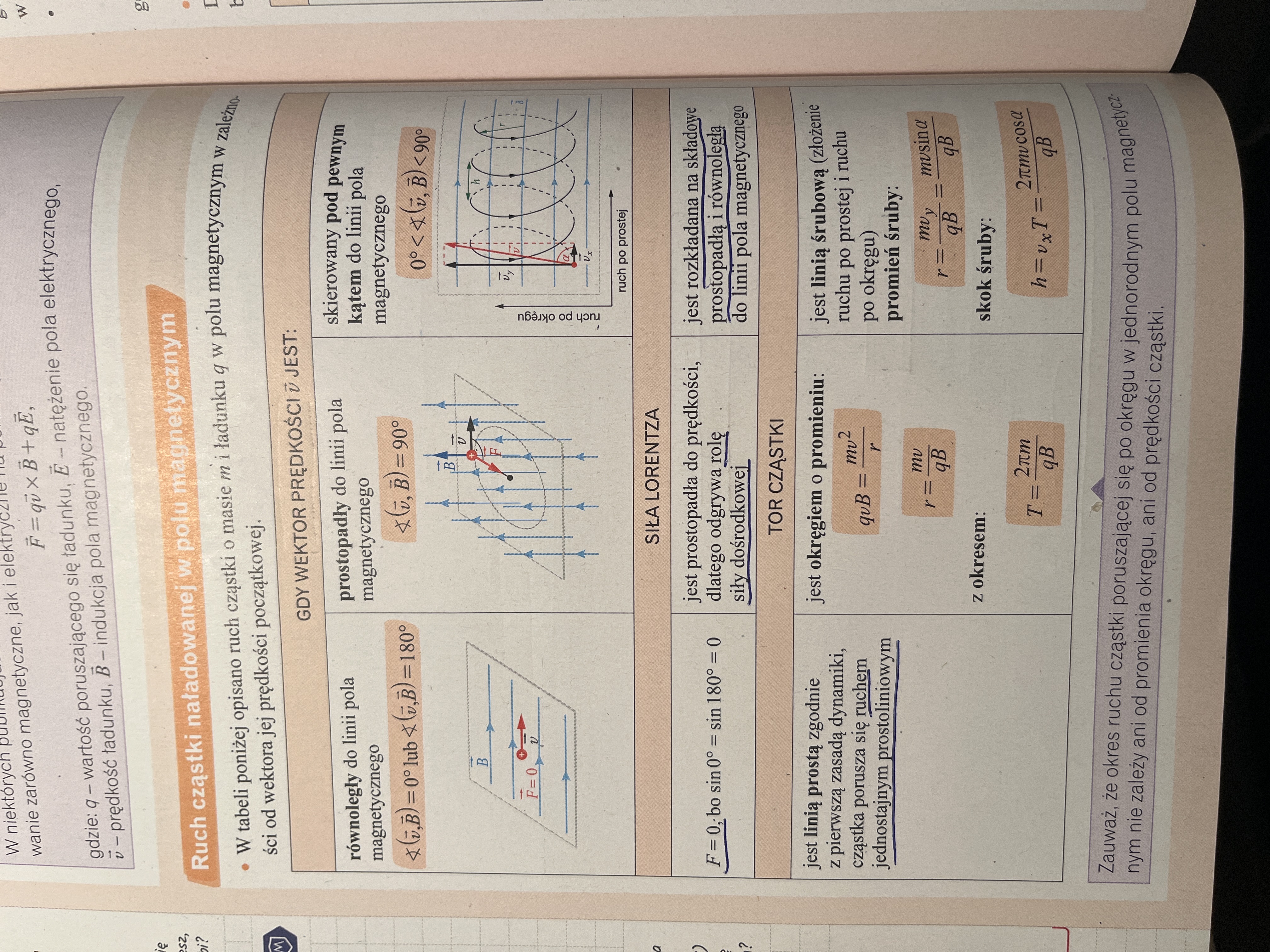
Prostopadle: mamy ruch po okręgu, więc możemy zapisać, że v = 2*pi*r/T, więc T = 2*pi*r/v. Z przyrównania siły dośrodkowej do siły Lorentza mamy to co jest już tam zapisane: qvB = mv^2/r, więc r = mv/qB. Możemy to wstawić do wyznaczonego wzoru na T i otrzymamy właśnie: T = 2*pi*m/qB (swoją drogą dokładnie takie rozumowanie przeprowadzaliśmy w ostatnim zadaniu na zajęciach nr 14 - polecam zerknąć na nagranie).

Inny kąt: promień wyprowadza się ponownie z przyrównania siły dośrodkowej do siły Lorentza, przy czym z uwagi na fakt, że okrąg znajduje się w płaszczyźnie prostopadłej do płaszczyzny rysunku, to prędkością cząstki w ruchu po tym okręgu nie jest cały wektor v, tylko jego składowa pionowa vy, którą można zapisać jak widać z prostej trygonometrii jako v*sin(alfa).

Skok śruby to z kolei odległość jaką wzdłuż osi linii śrubowej (czyli tu w kierunku poziomym) przebędzie cząstka po czasie jednego okresu. Ponieważ ruch w kierunku poziomym jest ruchem jednostajnym z prędkością vx = v*cos(alfa), to ten skok (czyli przebytą drogę) obliczymy jako iloczyn prędkości i czasu, który minął, a jak wspomniałem tym czasem jest jeden okres. Stąd skok h = vx*T = v*cos(alfa)* 2*pi*m/qB. Zauważmy, że sam okres jest taki sam jak w przypadku ruchu po okręgu, bo pokazaliśmy tam, że okres w ogóle nie zależy od prędkości.