zadanie 6

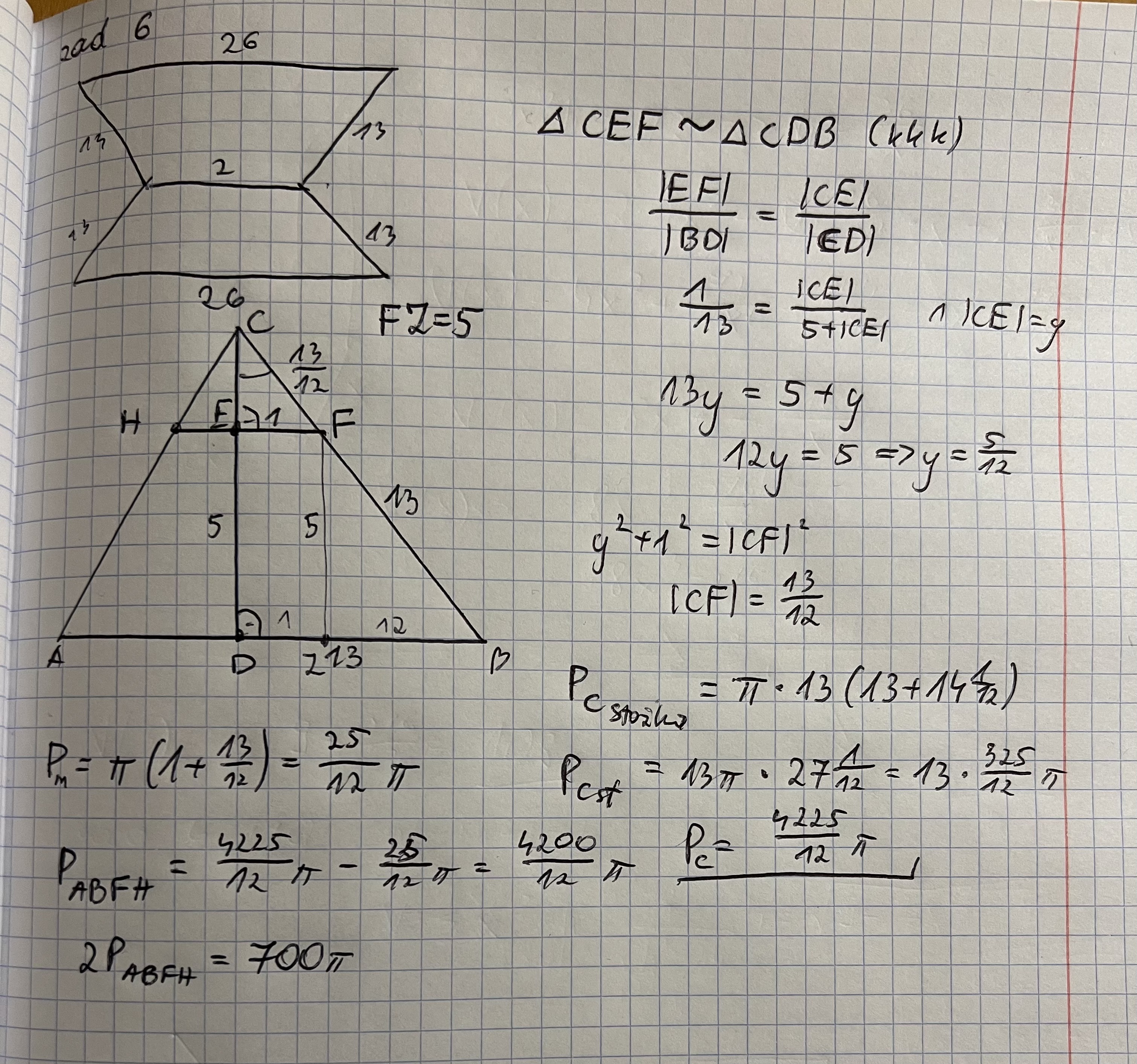
Gdzie jest błąd? Powinno wyjść 390 pi.
matematyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A mógłby pan wskazać w którym etapie mam błąd w moim rozumowaniu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
I dlaczego rozpatrujemy to jako walec i stożek? Podstawa walca to koło. Jeżeli byłby walec to potem nie mógłby być stożek chyba, ponieważ nie miałby w podstawie koła, tylko takie nierówne łuki. Więc chyba powinniśmy rozpatrywać prostopadłościan i stożek.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A mógłby pan wskazać w którym etapie mam błąd w moim rozumowaniu?
Aby odpowiedzieć na to pytanie - musisz dokładnie opisać w jaki sposób chciałaś obliczyć szukane wartości (tzn. logikę, która za tym stała).
Figura która powstaje to jest walec "bez stożków" (być może ta odpowiedź jest odpowiedzią również na twoje pierwsze pytanie).
Spójrz na rysunek.
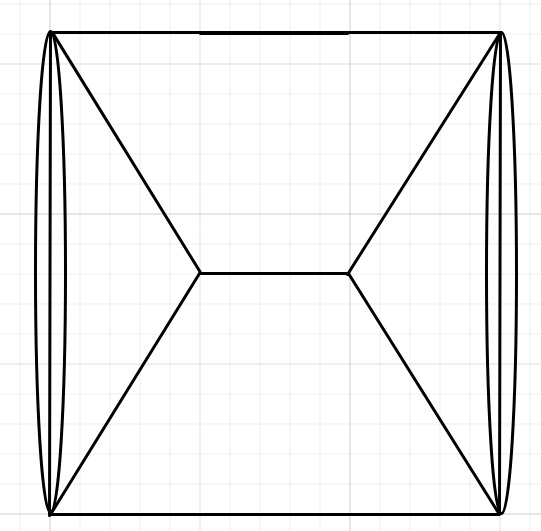
Żeby sobie to lepiej wyobrazić, możesz wyciąć sobie w papierze np. trapez i zacząć go obracać.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy wszystko jest już tutaj jasne ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Spróbuj innego podejścia:
- Powierzchnia otrzymanej brył powstaje tylko z obrotu tych boków trapezu, które nie leżą na osi obrotu (bo odcinek na osi nie tworzy żadnej bocznej powierzchni). Zatem obracają się:
- dłuższa podstawa CD=26
- dwa ramiona (każde o długości 13)
Powierzchnia boczna walca to:
S_walca=2pi*r*L=2*pi*5*26=260pi
Poweierzchnia z obrotu ramion:
Pole powierzchni bocznej takiego stożka to:
S_stożek = pi * promień * tworząca = pi * 5 * 13 = 65pi
W trapezie mamy dwa takie ramiona więc łączna powierzchnia z ich obrotu to 2 * 65 pi = 130 pi.
Suma pól: S_całk = 260pi+130pi=390pi