matura WFAIS UJ 2022 6.4 i 6.5
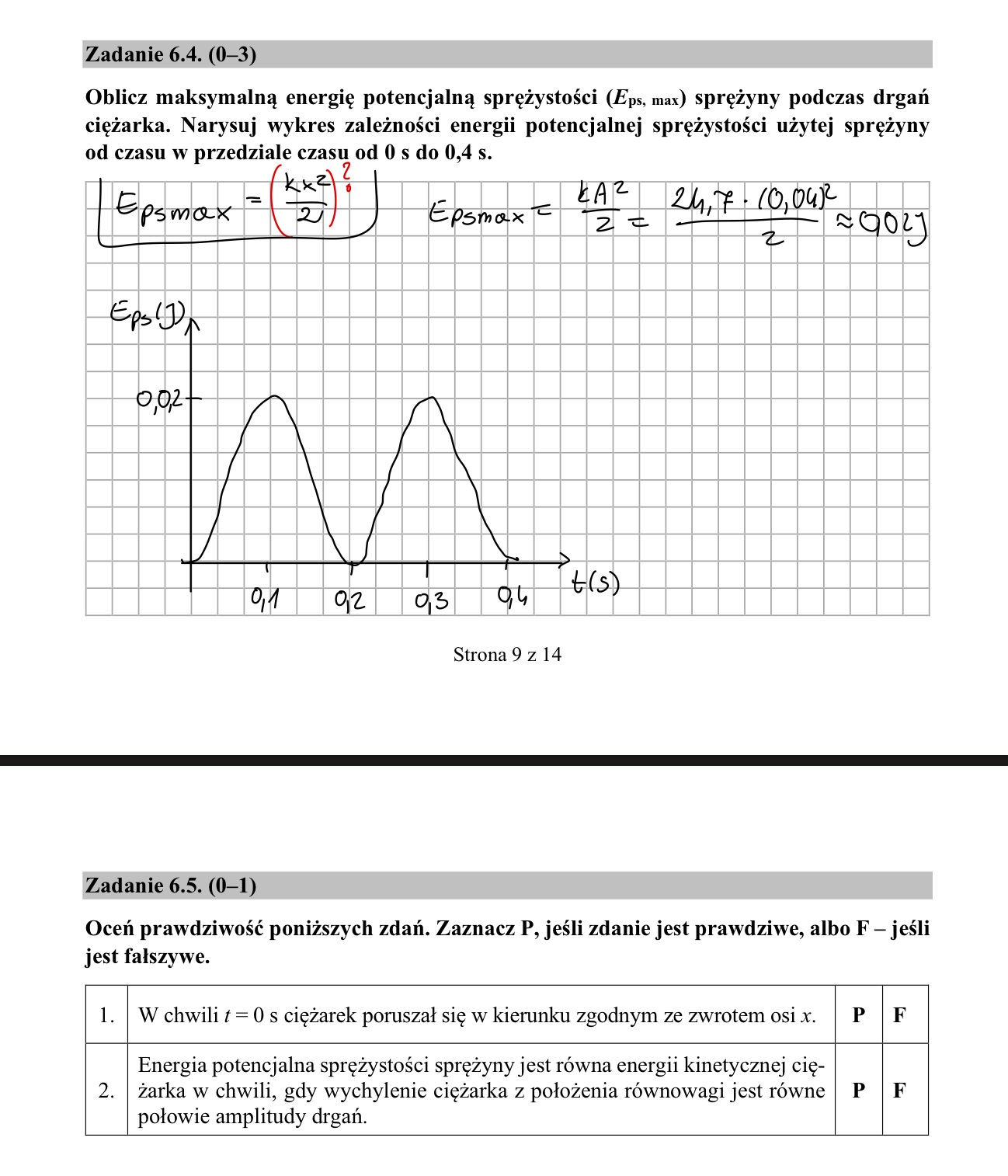
pp4) Czy energia potencjalna sprężystości nie wyraża się wzorem zaznaczonym przeze mnie w czerwony Nawias? dlaczego w odp użyto wzoru na energię całkowitą ?
skąd wiadomo jak jest charakter wykresu i w których momentach Eps osiąga wartości maxymalne
pp5) potrzebuję pomocy z oboma zdaniami, nie wiem po czym mam to stwierdzić :)
pf Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
super, dużo się wyjaśniło. jeszcze chciałabym się spytać, skad wywnioskować jak narysować wykres w pp 4? ( w ktorych momentach wartość maksymalna itp)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To świetnie :) co do wykresu, to zauważmy, że ponieważ Eps = kx^2/2, to maksymalne wartości Eps będzie przyjmować wtedy gdy x będzie maksymalny, czyli będzie to w momentach gdy ciało będzie maksymalnie wychylone z położenia równowagi. Na zajęciach z drgań (nr 17) mówiliśmy sobie, że wychylenie ciała z poł. równ. w ruchu harmonicznym jest maksymalne w tych samych momentach w czasie, gdy maksymalne jest przyspieszenie ciała. Z wykresu podanego w treści widzimy, że max. przyspieszenie mamy w 0,1 s; 0,3 s; 0,5 s itd. Stąd w tych momentach mamy również maksymalną Eps. Z kolei wtedy gdy przyspieszenie (i jednoczesnie wychylenie x) jest zerowe, wtedy Eps też jest zerowa.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
4) Oczywiście takim wzorem się ona wyraża. I jej maksymalna wartość to zatem 1/2 * k *A^2, więc jest to jednocześnie równe energii całkowitej :) dlatego w odpowiedziach od razu użyli tego wzoru na energię całkowitą.
5) Zdanie pierwsze - na początku ax miało wartość dodatnią, a to oznacza, że zwrot wektora przyspieszenia był zgodny ze zwrotem osi x. A wiemy, że wychylenie w ruchu harmonicznym jest zawsze przeciwnie zwrócone do przyspieszenia. Więc wychylenie x było na początku przeciwnie do osi x. Stąd mamy fałsz.
W zdaniu drugim mamy nieprawdę. Wiemy bowiem, że przy braku oporów Ek + Eps = 1/2 k*A^2. Widzimy natomiast, że w połowie maksymalnego wychylenia energia pot. sprężystości to Eps = 1/2 * k * (A/2)^2 - nie jest to połowa tej maksymalnej wartości, tylko jej 1/4, więc na Ek przypada 3/4 tej maksymalnej wartości, więc mamy znów fałsz.