Aksjomat Arkusz VII zadanie 7 wydanie 2024
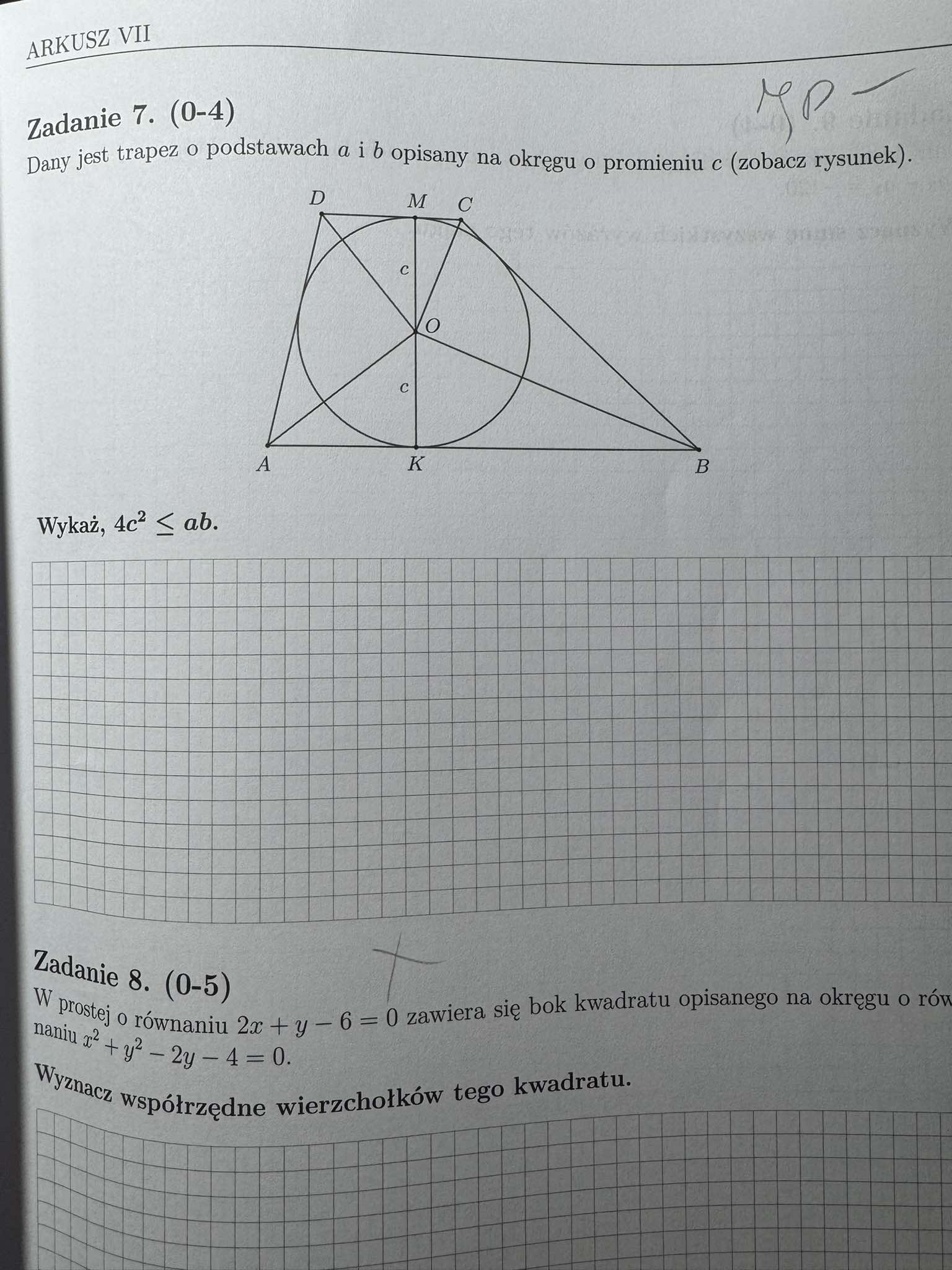

Nie mam pomysłu jak dojść do równania które prowadzi do dowodu... Rozumiem, że te trójkąty są podobne c^2 = xy to też ok, bo to wysokość w trójkacie prostokątnym, ale nie wiem jak dojść do równania, które otrzymujemy...
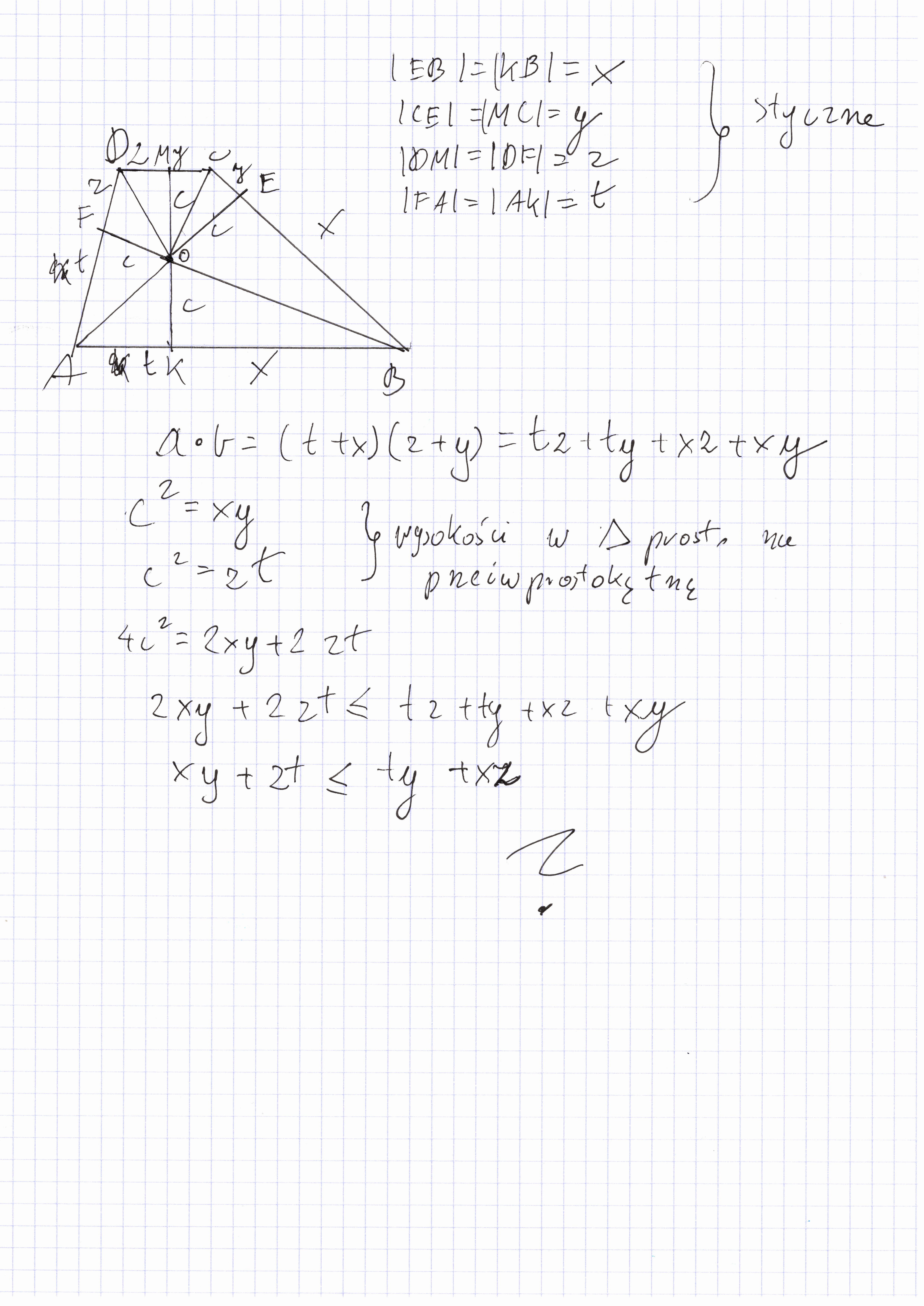
Planimetria Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie rozumiem jak otrzymujemy to brązowe równanie z pierwiastkami.
Bo jak mamy te dwa równania za które dostajemy 3 pkt to jak na załączonej kartce - dodaje je do siebie i potem mnożę x2. I dostaję coś zupełnie innego co nie wiem jak przekształcić do brązowego równania...

- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Z podobieństwa:
KB*MC= c^2 = AK*DM
Więc c = pierwiastek z (KB*MC) = pierwiastek z (AK*DM)
Więc c*c = c^2 = pierwiastek z (KB*MC)*pierwiastek z (AK*DM)
I obustronnie 4 możemy przemnożyć.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dobrze - to jest dla mnie jasne i zachodzi błąd w odpowiedziach - bo takie przekształcenie jak Pan zrobił jest dla mnie jasne. natomiast w odp. pomieszali boki i mnie trochę zmylili
Ale i tak mam kolejne pytanie - nawet jak zapiszemy poprawnie te przekształcenie (jak na skanie) - to jak uzasadnić, ze ten iloczynu po lewej stronie z pierwiastkami jest <= od iloczyny po prawej stronie dwóch podstaw?
Bo jak oni zapisali to z błędem to im wyszła nierówność średnich - jak natomiast zapisaliśmy tę nierówność poprawnie to znika możliwość nierówności średnich? Jak teraz to uzasadnić?

- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
OK wszystko jasne. Jakoś opornie przyszło mi to zadanie, ale ogarnięte. Dziękuję! :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
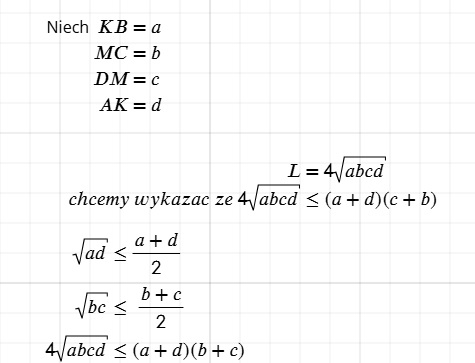
Które przejście konkretnie jest dla ciebie niezrozumiałe ?