Nowa Era, arkusz 2, zad.11

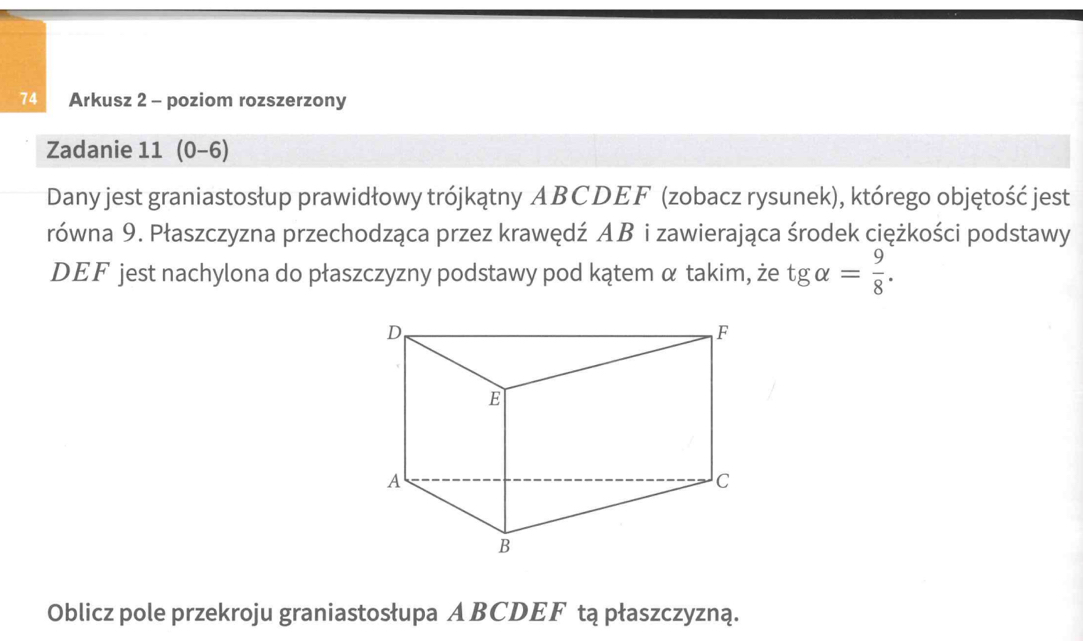
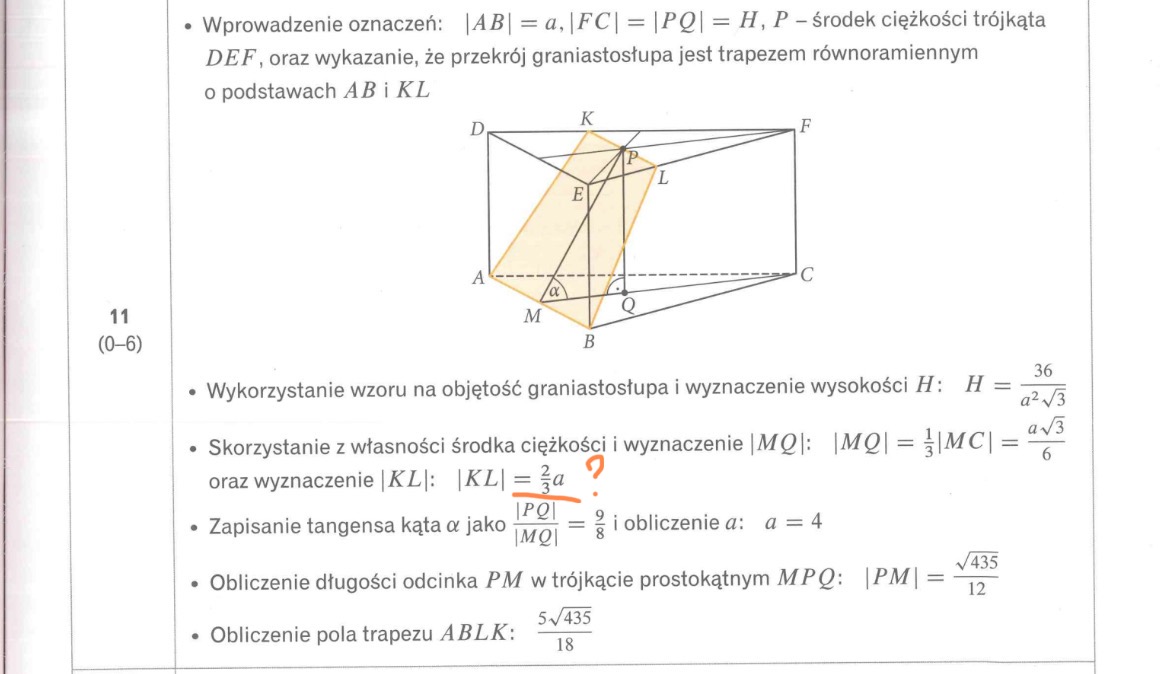
Graniastosłup prawidłowy trójkątny w swojej podstawie ma trójkąt równoboczny.

Płaszczyzna przechodzi przez krawędź AB, która jest równoległa do krawędzi DE, i wyznacza na ramionach DF i EF trójkąta równobocznego DFE dwa punkty, odpowiednio K i L, a więc odcinek KL również musi być równoległy do krawędzi DE.

Dodatkowo płaszczyzna ta przechodzić ma przez środek ciężkości podstawy, a więc przez środek ciężkości trójkąta równobocznego. Środek ciężkości trójkąta równobocznego leży na przecięciu się jego środkowych, czyli w tym przypadku też jego wysokości. Środkowe (tutaj: wysokości) dzielą się w stosunku 2:1. Zatem jeżeli na bok DE opada wysokość o długości h, to odcinek PF ma długość 2/3 h (h dzielę na 3 części i z racji podziału w stosunku 2:1, odcinek PF ma długość 2 z tych 3 części, więc 2/3 h).

Dodatkowo na mocy cechy (kkk), tutaj: kąt DFE jako kąt wspólny, oraz z równoległości KL || DE: |∠FDE|=|∠FKL| i |∠FED|=|∠FLK|, trójkąt FKL jest podobny do trójkąta FDE w skali k. Aby obliczyć skalę podobieństwa, można skorzystać z wysokości. Wysokość w trójkącie FKL ma długość 2/3 h, natomiast w trójkącie FDE ma długość h. Zatem skala podobieństwa k=(2/3 ⋅ h):(h)=2/3. Stąd już pozostaje wyliczyć długość boku KL: |KL|= 2/3 ⋅ |DE|, gdzie |DE|=|AB|=a, więc |KL|= 2/3 ⋅ a.

Dzięki wielkie, wszystko jasne :)