2011.3
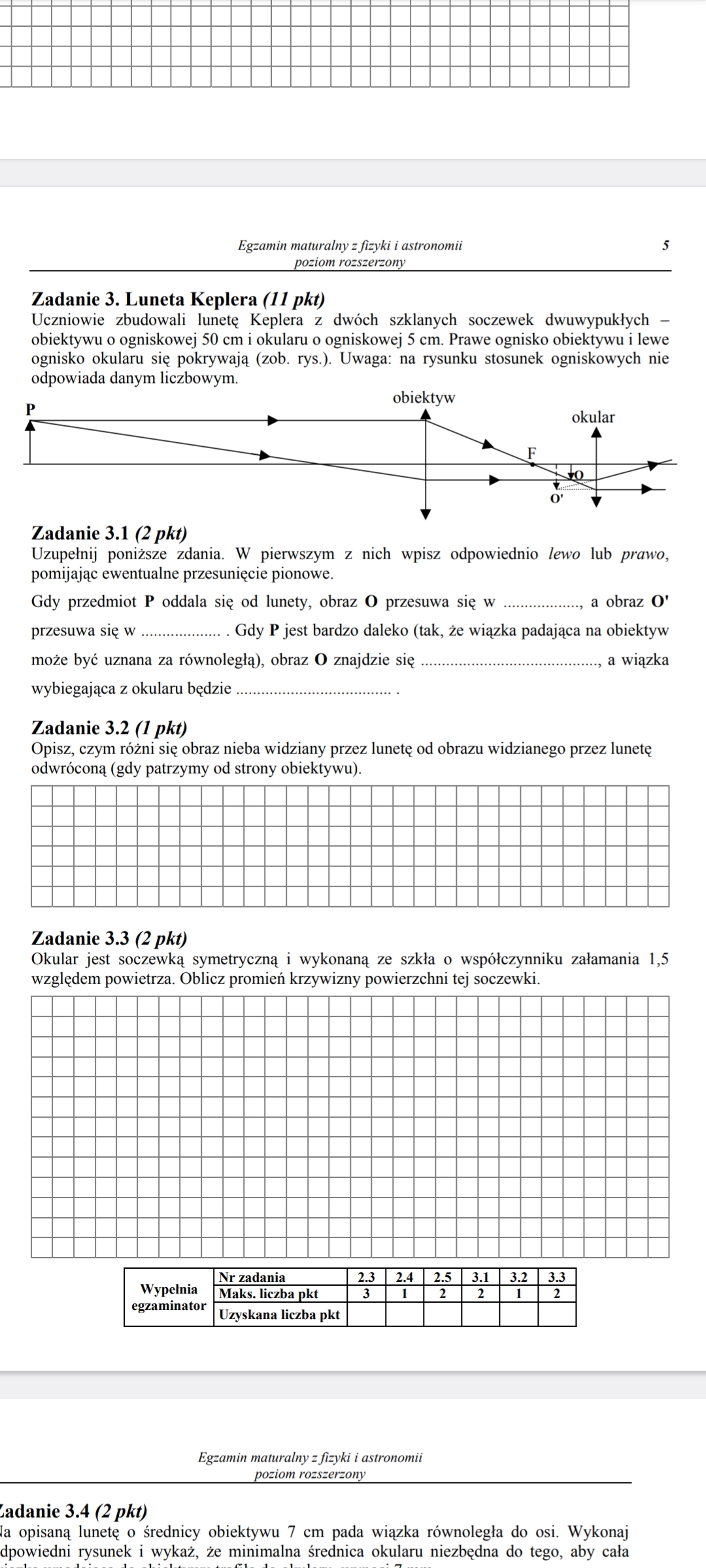


3.1.: Nie rozumiem jak zrobić ten podpunkt. Wydaje mi się, że przy oddalaniu się te promienie będą takie same.
3.2.: Dlaczego mam błąd? Odpowiedziałem na to pytanie patrząc na rysunek.
3.3.: Czy moja odpowiedź jest dobra? Bo u cke R=5cm i nie wiem czy to jest zaokrąglenie.
3.4 i 3.5: Czy te rozwiązania są poprawne? Bo cke pisze naokoło, że tak powiem. Przynajmniej takie mam wrażenie.
3.6: Czy tutaj N=20, bo N jest liczbą całkowitą? I to jest podobnie jak przy maksymalnych rzędach prążków w siatce dyfrakcyjnej? Że np jak by nawet wyszło N=19,00001 to byłoby Nmin=20?
Fizyka optyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1.: A nie da się tego jakoś sprytnie stwierdzić bez robienia 2 rysunków?
3.2.: Jak do tego dojść?
3.4.: Mam rysunek na prawo od odpowiedzi. Czy on by wystarczył?
3.5.: A jak można tutaj użyć tej mocy do obliczeń?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1: Można - skoro przedmiot P oddala się od lunety, to znaczy, że x rośnie. Z równania soczewki wynika zatem, że y musi zmaleć, a y to odległość obrazu O od obiektywu. Więc faktycznie obraz O przesuwa się w lewo. I na podstawie analogicznej analizy można będzie stwierdzić jak przesunie się wtedy O' (O jest przedmiotem dla okularu, a O' jest obrazem tego przedmiotu, tyle, że obrazem pozornym).
2: Tu znów można by to spróbować narysować, ale można też spróbować obliczyć - przyjmując np. takie wartości ogniskowych jak w zadaniu i przyjąć, że przedmiot P znajduje się bardzo daleko od lunety, można obliczyć powiększenie w jednym i w drugim przypadku (wykorzystując równanie soczewki i jak wspomniałem wyżej fakt, że w pierwszym przypadku obraz obiektywu jest przedmiotem dla okularu - po odwróceniu lunety będzie na odwrót) i zobaczymy, że powiększenie się w istocie zmniejszy. Natomiast są to żmudne trochę operacje i zdecydowanie nie będzie czegoś takiego na naszej maturze - o ile dobrze pamiętam w tej starej formule, do której dostosowane było to zadanie było w podstawie programowej wprost hasło luneta, więc uczeń w teorii powinien wtedy to wiedzieć. Teraz nie ma takiej potrzeby.
4: Widzę rysunek lunety, ale wg mnie należałoby tu jeszcze narysować bieg tych wiązek światła.
5: Jest to ładnie opisane w odpowiedziach, więc może nie będę tego tutaj dublował tylko pozwolę sobie zamieścić tu wyjątek z odpowiedzi CKE właśnie:
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1.: Co do drugiego zdania, piszą tam: "wiązka padająca na obiektyw może być uznana za równoległą"? Czy nie jest tak zawsze?
A w odpowiedziach jest, że powstaje on w punkcie F. W jaki sposób skoro dla x=f obraz nigdy nie powstaje dla soczewek skupiających? Jak stwierdzić, że wiązka wybiegająca z okularu będzie równoległa? Przy okazji dodatkowe pytanie czy obraz powstaje dla x=f w soczewce rozpraszającej?
I czy pokazałby Pan jak mniej więcej wyglądałyby rysunki do podpunktów 3.1 i 3.2?
3.4.: Czyli taki miałby być ten rysunek?
3.5: Skąd wiemy jaką średnicę ma oko? Rozumiem, że dalej wykorzystany jest wzór: I=P/S i ta moc promieniowania ma być stała? Co to znaczy, że coś zbiera więcej światła (jaka wielkość fizyczna za to odpowiada)?
Tak właściwie to które podpunkty z tego zadania mogłyby pojawić się na tegorocznej maturze?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1: No nie, jeśli przedmiot będzie blisko, to promienie z niego wychodzące, które będą trafiały w soczewką nie będą biegły równolegle do osi optycznej. Co do drugiego zdania - to obraz powstaje w przybliżeniu w punkcie F, a nie przedmiot znajduje się w F (a to właśnie gdy przedmiot znajduje się w f to obraz nie powstaje). Co do równoległości wiązki - jeśli zakładamy już, że promienie wychodzące z P są równoległe do osi optycznej, a zgodnie z treścią ogniska obiektywu i okularu się pokrywają, to te promienie po przejściu przez obiektyw przechodzą przez ognisko obiektywu i jednocześnie okularu, czyli po przejściu przez okular te promienie z powrotem muszą być równoległe do osi optycznej.
I tak, w przypadku soczewki rozpraszającej obraz powstanie nawet gdy przedmiot będzie w ognisku (czyli x = f).
3.4: Taki, czyli jaki? ;)
3.5: Twórcy sobie założyli, że taką właśnie średnice ma oko. I tak, P jest stałe. A to, że luneta zbiera więcej światła wiąże się z tym, że obiektyw ma większą powierzchnię od oka, więc po prostu więcej promieni świetlnych w niego trafia.
Na pewno podpunktu 3 - 6, 1 i 2 pewnie wtedy gdyby dopisali trochę więcej informacji.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1.: A jakie będą te promienie, które znajdą się blisko soczewki?

Zakładam, że górny promień na rysunku w treści zadania nie jest "bardzo daleko" a jednak jest on równoległy do osi optycznej soczewki.
Jak stwierdzić, że ten obraz powstanie w punkcie F?
3.2.: Czyli da się jakoś w prosty sposób dojść do poprawnej odpowiedzi?
3.4.:
3.5. Czyli średnica obiektywu to średnica lunety a średnica oka to średnica okularu? Czy na symbolach po prawej dobrze to zapisałem?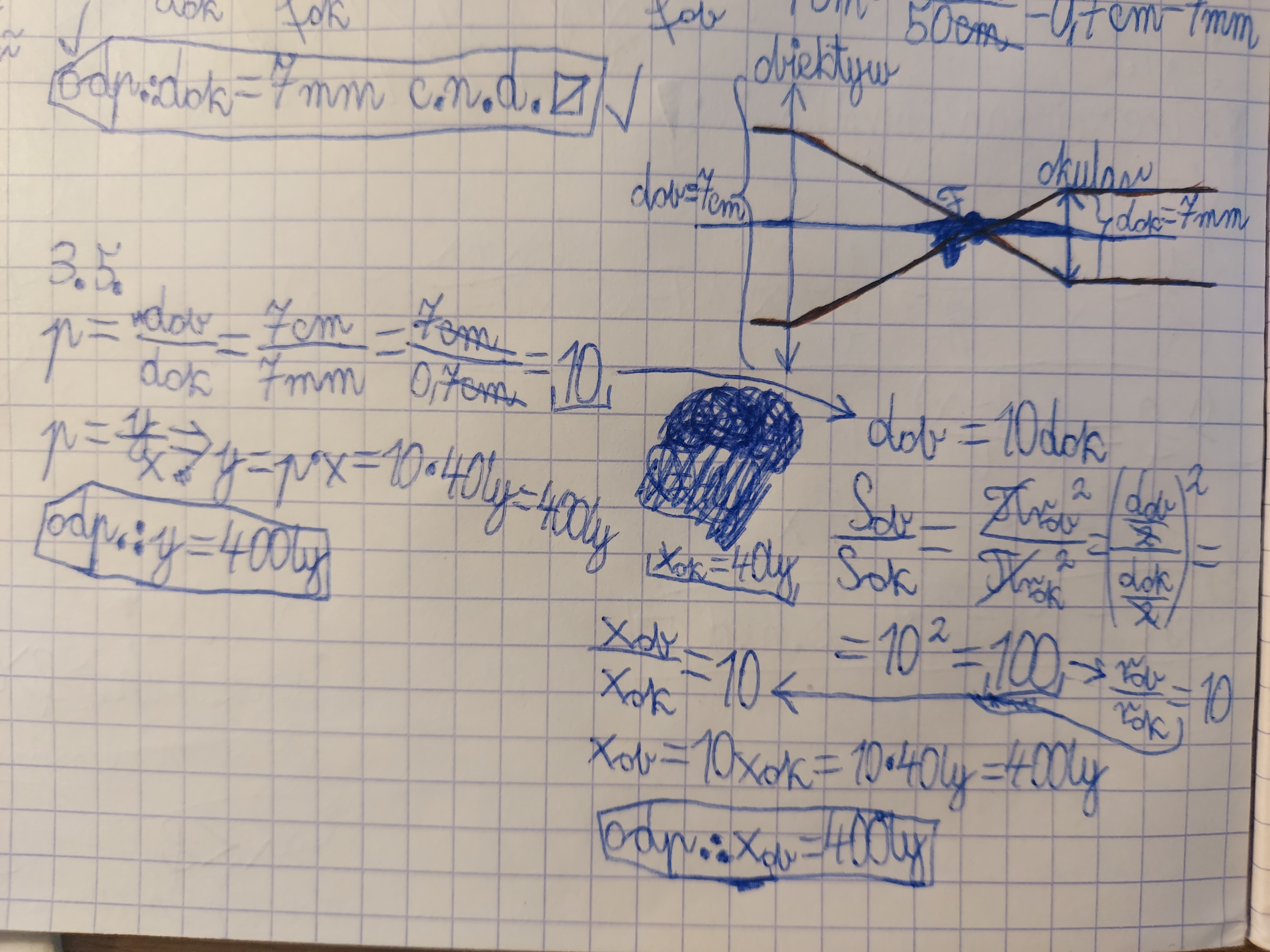
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1: Ale zauważ, że jeśli przedmiot P będzie "bardzo daleko" (a przecież luneta służy do obserwowania właśnie takich przedmiotów), to każdy promień świetlny docierający z przedmiotu P do soczewki będzie w bardzo dobrym przybliżeniu równoległy do osi optycznej (a nie tylko ten jeden górny). A w przypadku przedmiotu położonego blisko soczewki na pewno każdy promień taki nie będzie.
To, że obraz powstanie w przybliżeniu w F można łatwo pokazać z równania soczewki. Gdy x jest bardzo duże, to y wychodzi niemalże równe f.
3.2: No tak jak napisałem wcześniej obliczeniowo można to pokazać, nie widzę tak teraz prostszego sposobu.
3.4: Tak.
3.5: No nie, średnica obiektywu to średnica obiektywu, a średnica okularu to średnica okularu ;) to są po prostu dwie różne soczewki wchodzące w skład lunety ;) a że średnica oka wynosi 5 cm to oni sobie tak dla uproszczenia przyjęli. Mogliby przyjąć, że to jest np. 3 cm, tylko wtedy liczbowo to wychodziłoby nie tak ładnie ;) Ale tak, wygląda na to, że symbolicznie jest to u Ciebie przy tych oznaczeniach poprawnie zapisane.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1.: Czyli ta równoległość wynika jakoś z trygonometrii? Np. cos alfa rośnie, więc alfa maleje?
3.2.: A pokazałby Pan mniej więcej jakby wyglądało to obliczenie, gdy obrócimy lunetę? Bo przed obróceniem to rozumiem, że wychodzi y=f.
3.5.:"Jeśli luneta ma 10-krotnie większą średnicę niż oko..." - z tego zdania dla mnie wynika, że oko ma średnicę 7mm (taką jak okular) a luneta 7cm (taką jak obiektyw).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1: Hmm, nie wiem o jakich kątach mówisz. Ale to nieważne. Wyobraź sobie, że przedmiot P (którego dolny koniec leży na osi optycznej, a górny nie jakoś bardzo daleko od osi optycznej zgodnie z tym co tu mamy) ustawiasz 100 metrów na lewo od tej soczewki, którą masz na kartce. I chcesz narysować promienie wychodzące z P, które jednocześnie trafiają w soczewkę. Zauważ, że będą one niemal równoległe do osi optycznej.
3.2: Tylko zauważ, że tu dwa razy musisz policzyć y dla każdego ustawienia. Przyjmij, na początku że powiedzmy x = 100 m. Wtedy rozpatrując na początek sam obiekty wyjdzie Ci jakieś y. I teraz to będzie położenie przedmiotu dla okularu. Czyli będziesz miał teraz jakieś nowe x dla okularu i dla okularu teraz wyliczasz y. I dopiero teraz masz to finalne y w pierwszej konfiguracji. Możesz policzyć powiększenie (ten finalny y podzielić przez te na początku założone 100 m). A potem odwróć sytuację - czyli przyjmujesz drugą konfigurację (odwracasz lunetę), tzn. znowu możesz sobie przyjąć, że początkowy x = 100 m, ale teraz najpierw obliczasz y dla okularu - to gdzie wyjdzie Ci obraz da Ci od razu położenie przedmiotu dla obiektywu. I dla takiego położenia przedmiotu obliczasz y dla obiektywu - i to będzie ten finalny y w drugiej konfiguracji. I znów możesz policzyć powiększenie i wyjdzie ono mniejsze niż w pierwszej konfiguracji. Ale szczerze mówiąc nie widzę wielkiego sensu w nadmierne zagłębianie się w te obliczenia, czegoś takiego nie będzie trzeba robić na naszej maturze ;)
3.5: Sorrki, nie wiem czemu wcześniej wkręciłem sobie, że przyjęli, że średnica oka to 5 cm. No to faktycznie, patrząc na to co napisali to faktycznie przyjęli takie nazewnictwo jak mówisz, wcześniej nie doczytałem tego dokładnie. Ale zdecydowanie nie jest to żadne oficjalne nazewnictwo.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1.: Ale to rozumowanie zadziała chyba tylko wtedy gdy przyjmiemy, że soczewka jest dosyć mała w porównaniu do 100m.
3.2.: Czyli tak na logikę można napisać, że patrząc od strony okularu obraz będzie powiększony, a od strony obiektywu pomniejszony?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1: Oczywiście tak, ale nie znam lunet, których rozmiary byłyby porównywalne do 100 m ;) A poza tym z reguły ogląda się za pomocą lunety obiekty zdecydowanie bardziej odległe niż 100 m.
3.2: W rzeczywistości w obu przypadkach obraz będzie pomniejszony, ale w istocie większe powiększenie uzyskamy, gdy będziemy oglądali to od strony okularu.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.2.: Czy to wynika z tego, że średnica okularu jest mniejsza niż obiektywu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bezpośrednio z tego, że ogniskowa okularu jest mniejsza niż obiektywu (choć jest to związane z różnicą średnic tych soczewek).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Heh no tak, tak to można nazwać ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
3.1: Najprościej jest zrobić sobie dwie konstrukcje dla różnych odległości i zobaczysz, że obraz jednak się przesunie (trzeba to zrobić możliwie dokładnie).
3.2: No cóż, Ty nawet nie odpowiedziałeś na pytanie postawione w treści - pytanie jest o to czym różnią się dwa obrazy, a Ty podałeś cechę któregoś z obrazów. Tu trzeba by w ogóle zauważyć, że w takiej konfiguracji jaka jest przedstawiona, ludzkie oko znajduje się po prawej stronie układu i widzi obraz O'. Trzeba by się zastanowić co by było gdyby lunetę odwrócić (zgodnie z treścią) - okaże się, że właśnie np. powiększenie obrazu widzianego ludzkim okiem się w takiej sytuacji zmieni.
3.3: Niepotrzebnie w ogóle tu używałeś wzoru na 1/f = 1/f1 + 1/f2. Mamy tu przecież obliczyć ogniskową okularu - zajmujemy się tu tylko jedną soczewką, więc wystarczający jest ten wzór z promieniami. I wyjdzie wtedy dokładnie R = 5 cm.
3.4: Wygląda ok, tylko, że trzeba było tu jeszcze zrobić rysunek.
3.5: Liczbowo się to zgadza, ale jednak nie jest to w mojej opinii wystarczające uzasadnienie, zwłaszcza, że w treści podana jest nawet wskazówka co decyduje o możliwości zobaczenia gwiazdy, a jest to moc promieniowania - Ty tej wielkości w ogóle tu nie wykorzystujesz.
3.6 Tak jest - liczba fotonów czy liczba prążków to są liczby całkowite, więc nie możemy używać ułamkowych ich wartości (nie ma czegoś takiego jak np. połowa fotonu ;)) Kwestia w którą stronę zaokrąglać zależy już od treści, tu pytają o to ile przynajmniej fotonów musiałoby wpaść do ludzkiego oka, skoro wychodzi, że wartością graniczną jest 19,4 to znaczy że 19 fotonów byłoby liczbą niewystarczającą, bierzemy więc 20.