Zadanie domowe 24 cz.1 zad.7
Na ostrosłupie prawidłowym trójkątnym opisano kulę o promieniu 6. Wykaż, że ten ostrosłup jest czworościanem jeśli wiadomo, że ma objętość największą z możliwych. Oblicz tę objętość.
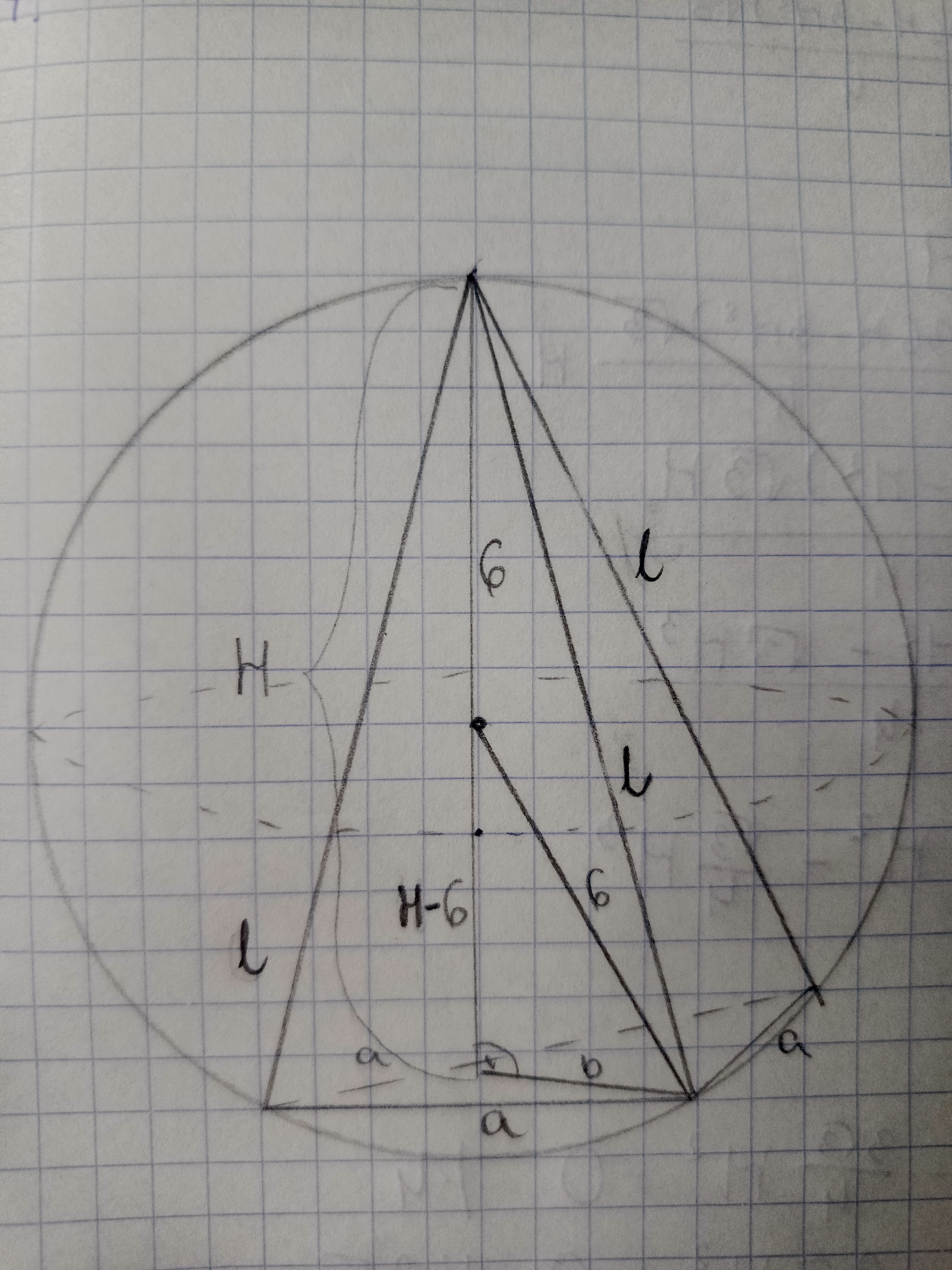
Mam pytanie co do dziedziny w tym zadaniu. Optymalizowałam objętość jako funkcję V(H), gdzie H to wysokość tego ostrosłupa. Obliczyłam dziedzinę i otrzymałam H∈(0,12) i właśnie tego nie jestem pewna, bo wszystkie odcinki muszą istnieć i nie wiem czy powinnam dodać jeszcze nierówność H-6>0, bo gdyby teoretycznie podstawa ostrosłupa leżała nad środkiem kuli, to wówczas H<6, czyli H-6<0.
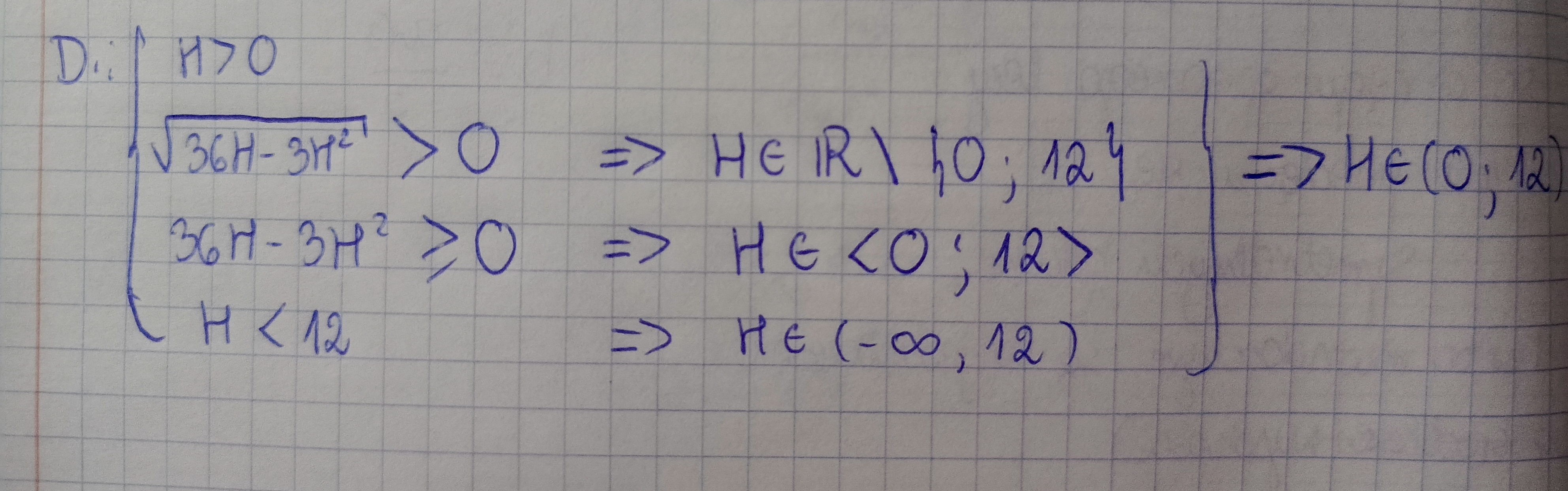
Matematyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Proszę Pana, a dlaczego nie trzeba uwzględniać przypadku, że podstawa ostrosłupa leży nad środkiem kuli i wtedy H<6, bo trochę nie rozumiem?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zgadza się, w takim przypadku H może być mniejsze od 6 wtedy dziedzina jest taka jak w twoim pierwotnym rozwiązaniu. Można też rozważyć od początku dwa przypadki.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jak wyszlo ci w 2) nierownosci ze Hnalezy do R bez 0 i 12?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli, proszę Pana, którą dziedzinę (0,12) czy (6,12) powinnam przyjąć w tym zadaniu, bez napisania, że rozważam oddzielnie dwa przypadki, ale w rozwiązaniu jednocześnie nie wykluczając możliwości, że podstawa ostrosłupa leży nad środkiem kuli?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jakub, jak tak teraz patrzę to faktycznie w tej drugiej nierówności powinien być przedział (0,12), dzięki:)
Pierwiastek jest zawsze ≥ 0, więc tutaj chyba mogłam dać też √(36H-3H²)≠0 i wtedy byłoby to takie rozwiązanie, a to że wartość podpierwiastkowa jest ≥ 0 zapewniłaby wówczas trzecia nierówność 36H-3H²≥0.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale w przypadku największej objętości można też pokazać, że ten drugi przypadek o którym piszesz nie musi być rozpatrywany
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Proszę Pana, jak wówczas należałoby to pokazać?
I czy jeśli nie wykazałabym tego, ale też nie rozpisałabym zadania na 2 przypadki oddzielnie (nie wykluczając w rozwiązaniu możliwości, że podstawa ostrosłupa leży nad środkiem kuli) to którą powinnam wtedy przyjąć dziedzinę (0,12) czy (6,12)?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W każdym przypadku inna dziedzina, nie może być jednej dziedziny dla wszystkich przypadków :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dobrze, dziękuję:)
Proszę Pana, jak w takim razie należałoby pokazać, że drugi przypadek, w którym podstawa ostrosłupa leży nad środkiem kuli, nie musi być rozpatrywany?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
H-6>0 jeszcze powinno być.