Fizyka prawo załamania
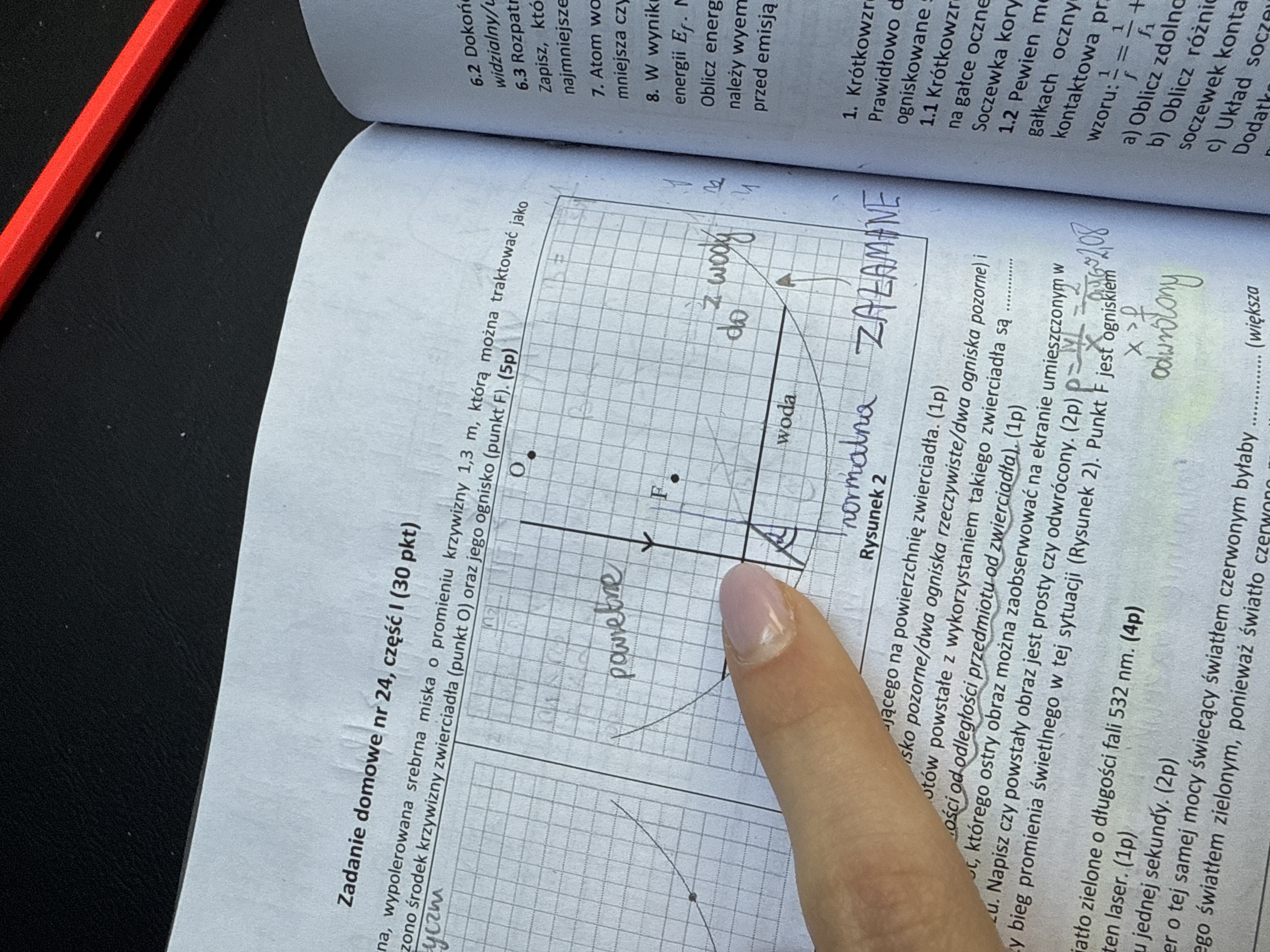
Dlaczego tutaj przy przejściu z ośrodka (powietrze) do wody w pierwszą stronę nie ma załamania, a w drugą jest?
kiedy mam stosować prawo załamania?
wytłumaczy ktoś czemu B>L
mi wychodzi odwrotnie że kąt załamania jest mniejszy niż kąt padania
Fizyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Moje obliczenia to:
kąt padania/kąt załamania (beta ten który dorysujemy) =nzałamania/npadania
n załamania jest większe niż 1 (bo to woda), a npadania = 1 (bo to powietrze), a więc
kąt padania> kąt załamania
Dlaczego u Pana n są odwrotnie? W karcie jest n2/n1
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No właśnie, trzeba wiedzieć, które n za co odpowiada. W karcie jest n2/n1, bo jakoś to musieli zapisać, ale należy pamiętać, że to które n jest które zależy od tego z którego ośrodka przechodzimy do którego. W przypadku załamania ośrodkiem o n1 będzie ośrodek, z którego światło wychodzi, a ośrodkiem o n2 będzie ośrodek, do którego światło wchodzi. Jeśli zatem rozpatrujemy teraz załamanie przy przejściu światła z wody do powietrza, to n1 to współczynnik załamania dla wody, a n2 to współczynnik załamania dla powietrza.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A w tym drugim wzorze z karty wzorów jak rozpoznać te n współczynniki załamania? Bo wiem, że tam jest chyba na odwrót?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jak rozumiem pytasz o ten wzór z karty dla całkowitego wewnętrznego odbicia - tam w istocie nazewnictwo jest odwrotne, więc może ono byc trochę mylące, natomiast na szczęście w opisie tego wzoru napisali, który współczynnik jest związany z którym ośrodkiem:
Czyli oni tu zakładają, że światło "próbuje" przejść z ośrodka o współczynniku n2 do ośrodka o współczynniku n1.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dlatego, że w pierwszym przypadku kąt padania to 0 stopni. I jeśli tak jest, to kąt załamania w tym szczególnym przypadku też wychodzi równy 0 stopni, więc nie zmienia się akurat kierunek biegu promienia załamanego. A w każdym innym już tak, dlatego przy wyjściu już ten kierunek się zmienia (bo tam kąt padania zerowy nie jest).
A to że przy wyjściu światła z wody do powietrza kąt załamania jest większy niż kąt padania wynika wprost z prawa załamania właśnie. Możemy zapisać, że sin(alfa)/sin(beta) = n_pow/n_wody. Ponieważ n_wody > n_pow, to beta > alfa.