zadnia info arkusz 27kwietnia 2024 zad 9
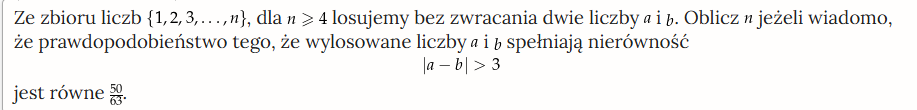
nie wiem nawet od czego zacząć to zad oprocz omegi combinacja 2 z n
kombinatoryka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Miałem na myśli tak abyś zrobił to bez zliczania ręcznego przypadków.
W takim razie pokażę jak powinno to być zrobione:
Załóżmy, że n=10.
1. Obliczamy liczbę wszystkich możliwych par spośród 10 elementów.
(28 po 2)
2. Zamiast liczyć bezpośrednio pary spełniające |a-b|>3 liczymy ich dopełnienie czyli liczbę par |a-b|<=3
Par z różnicą równą 1: (1,2), (2,3).. jest 9
Par z różnicą równą 2: (1, 3), (2,4) .. jest 8
Par z różnicą równą 3 jest (1,4) (2, 5)... 7
Zatem liczba par spełniających |a-b|>3 to pozostałe pary czyli (10 po 2) - 25
Teraz możemy obliczyć prawdopodobieństwo.
Teraz w naszym zadaniu wystarczy, że za przykładowe "10" podstawisz "n" i ułożysz odpowiednie równanie tzn.
Wyrażenie z "n" = 50/63
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
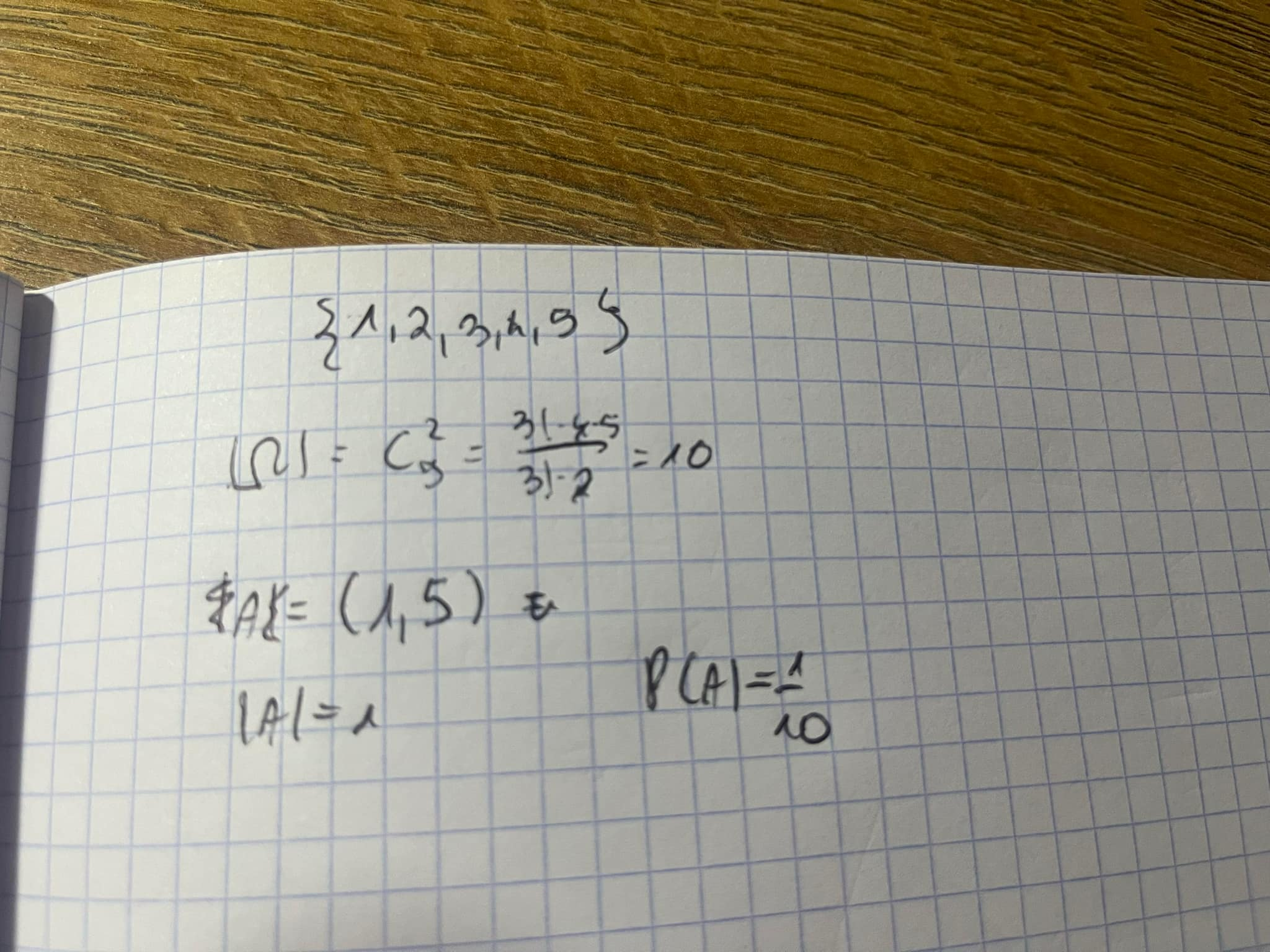
Spróbuj rozwiązać poniższy przykład.
Ze zbioru liczb {1, 2, 3, 4, 5} losujemy bez zwracania dwie liczby a i b. Oblicz prawdopodobieństwo tego, że wylosowane liczby a i b spełniają nierówność |a-b| > 3