Zad.INF.18
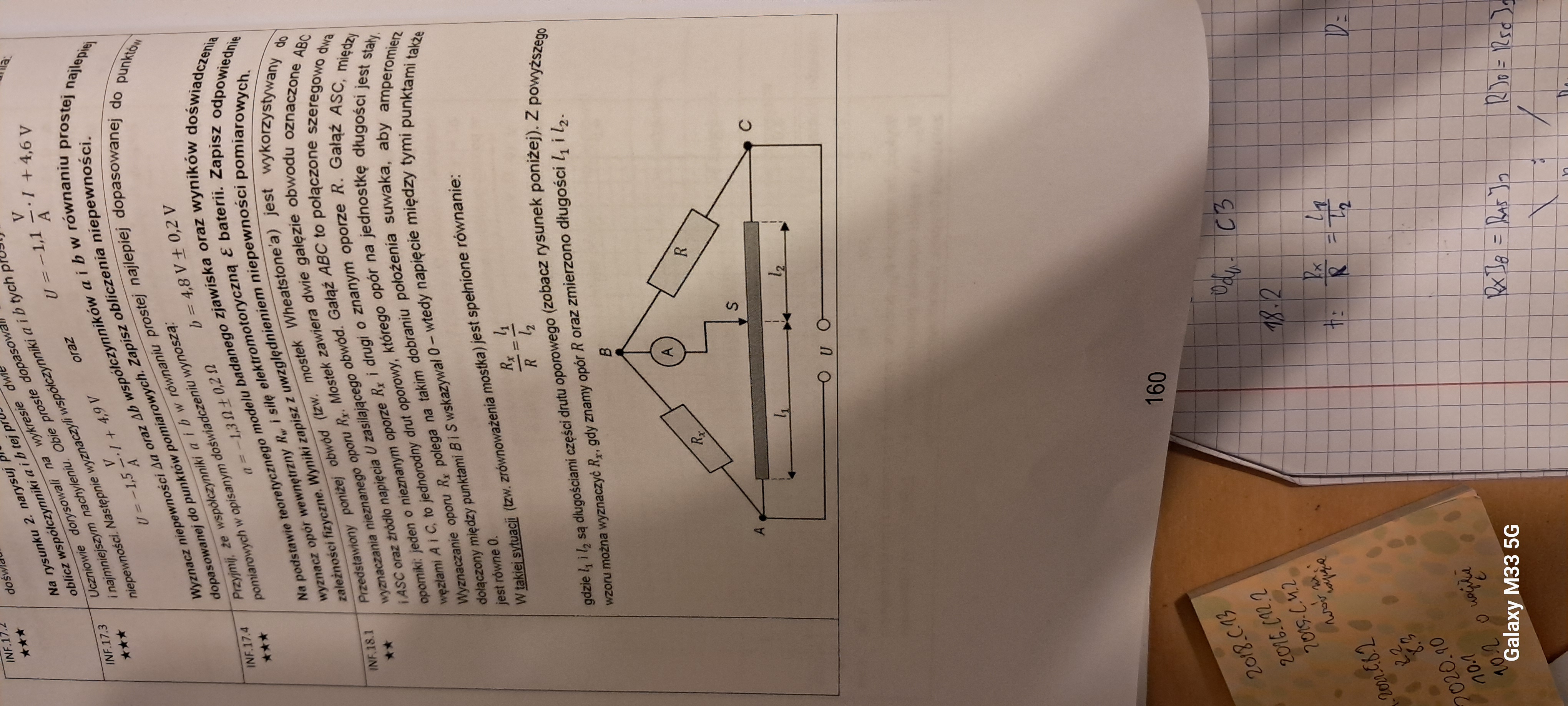
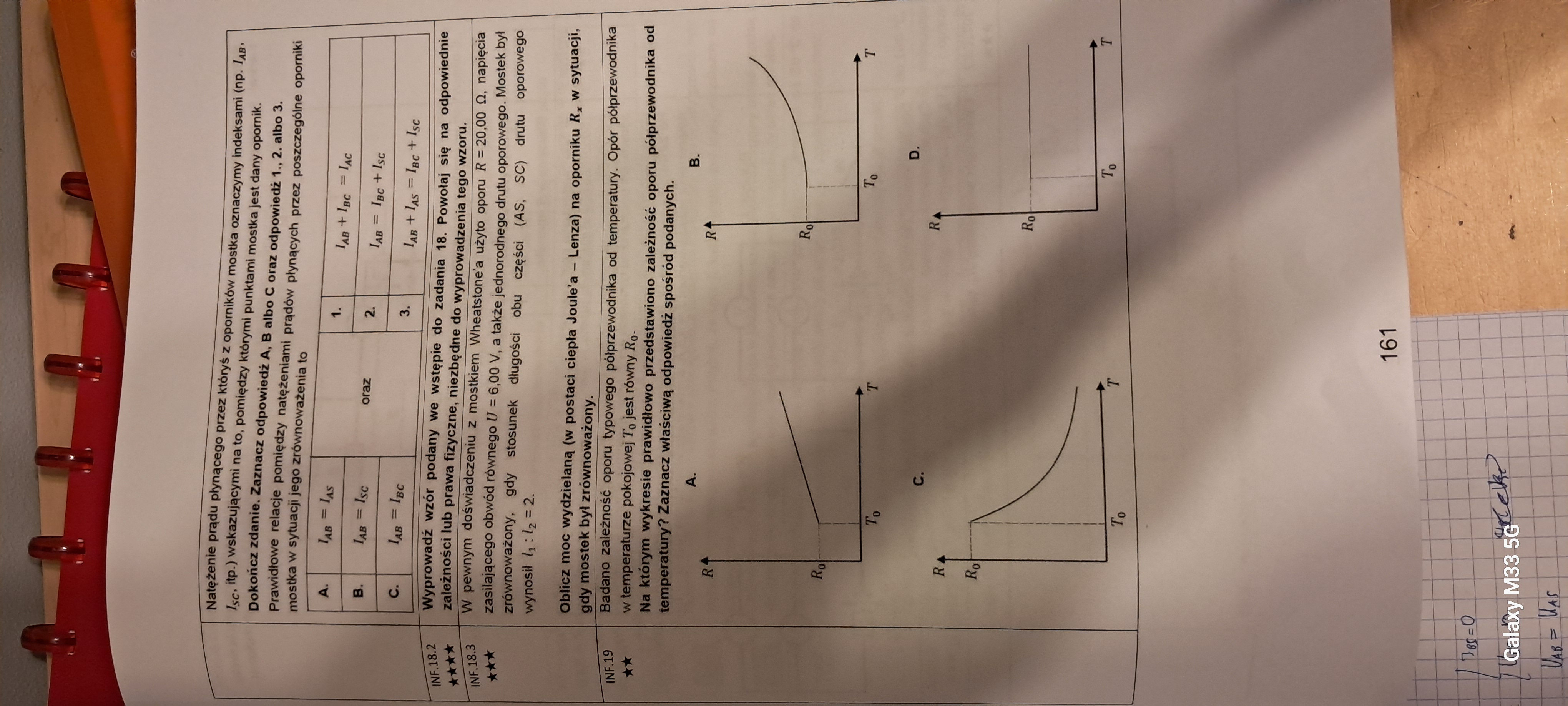
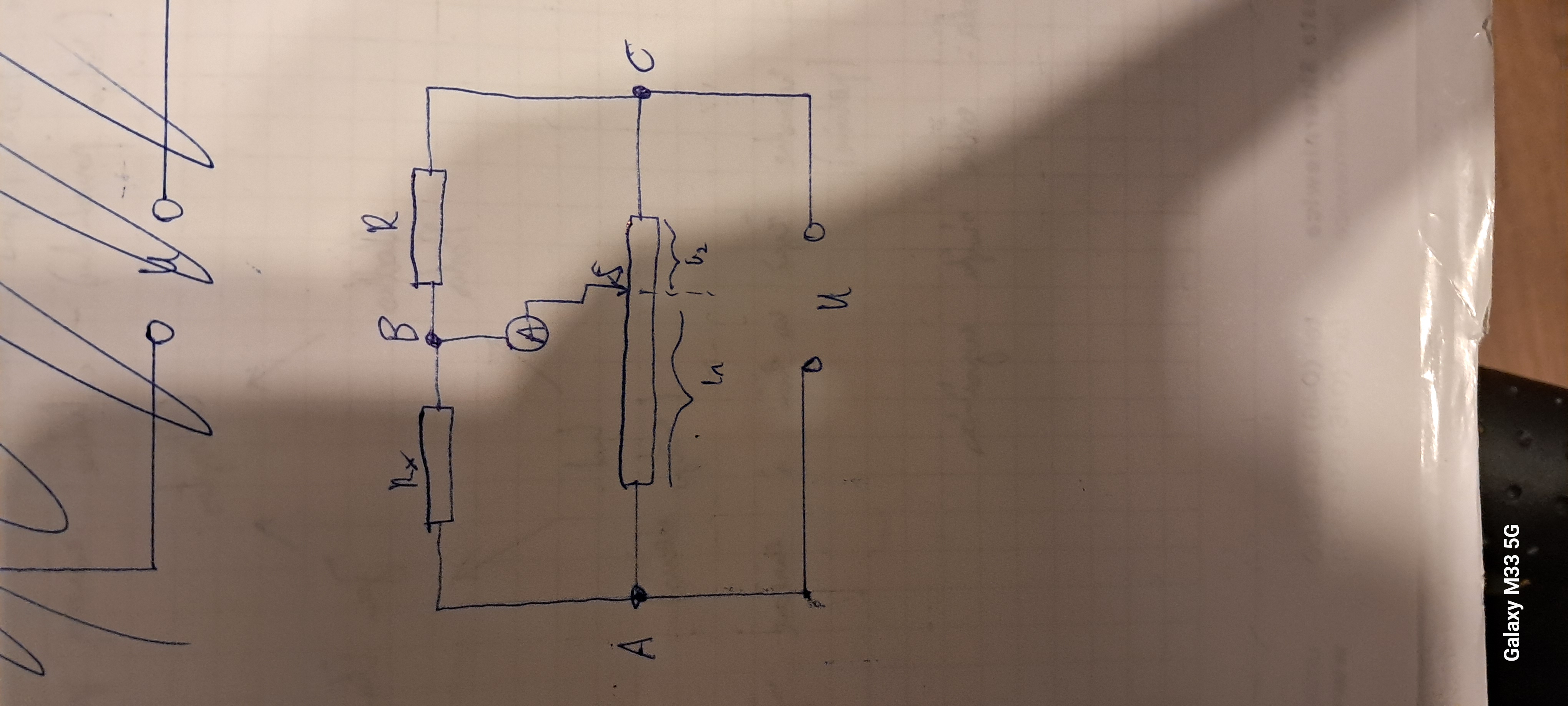
Czy ten rysunek można sprowadzić do innej postaci, takiej jaka jest na moim zdjęciu?
18.1
Czy odpowiedź 3. Jest poprawna ponieważ Ias=Isc i Iab=Ibc więc jak przerzucimy na drugą stronę to wyjdzie nam 0=0?
18.2
Potrafię zrozumieć że U=Uac bo to równoległe gałęzie oraz, że Uac=Uab+Ubc (bo to tłumaczę sobie tak że jakby spojrzeć na mój nowy rysunek, o ile jest poprawny to niejako Uac II U i to jest równolegle do Uabc). Ale skąd wiadomo, że Uab=Uas i Ubc=Usc? Nie bardzo rozumiem co ten punkt S wnosi skoro od punktu B do S nie płynie prąd, więc ja to traktuje jakby tam nic nie było.
Fizyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Hmm… jakoś jeszcze nie rozumiem, ale popatrzyłem na to zadanie na świeżo jeszcze raz i czy ja mogę sobie dodać punkty D i E i one są jakby przedłużeniami A i C więc traktuje D=A i E=C i teraz łatwo można zobaczyć że Udb=Uas i Ube=Usc (teraz ewidentnie widzę że B i S dzieli na dwie równoległe)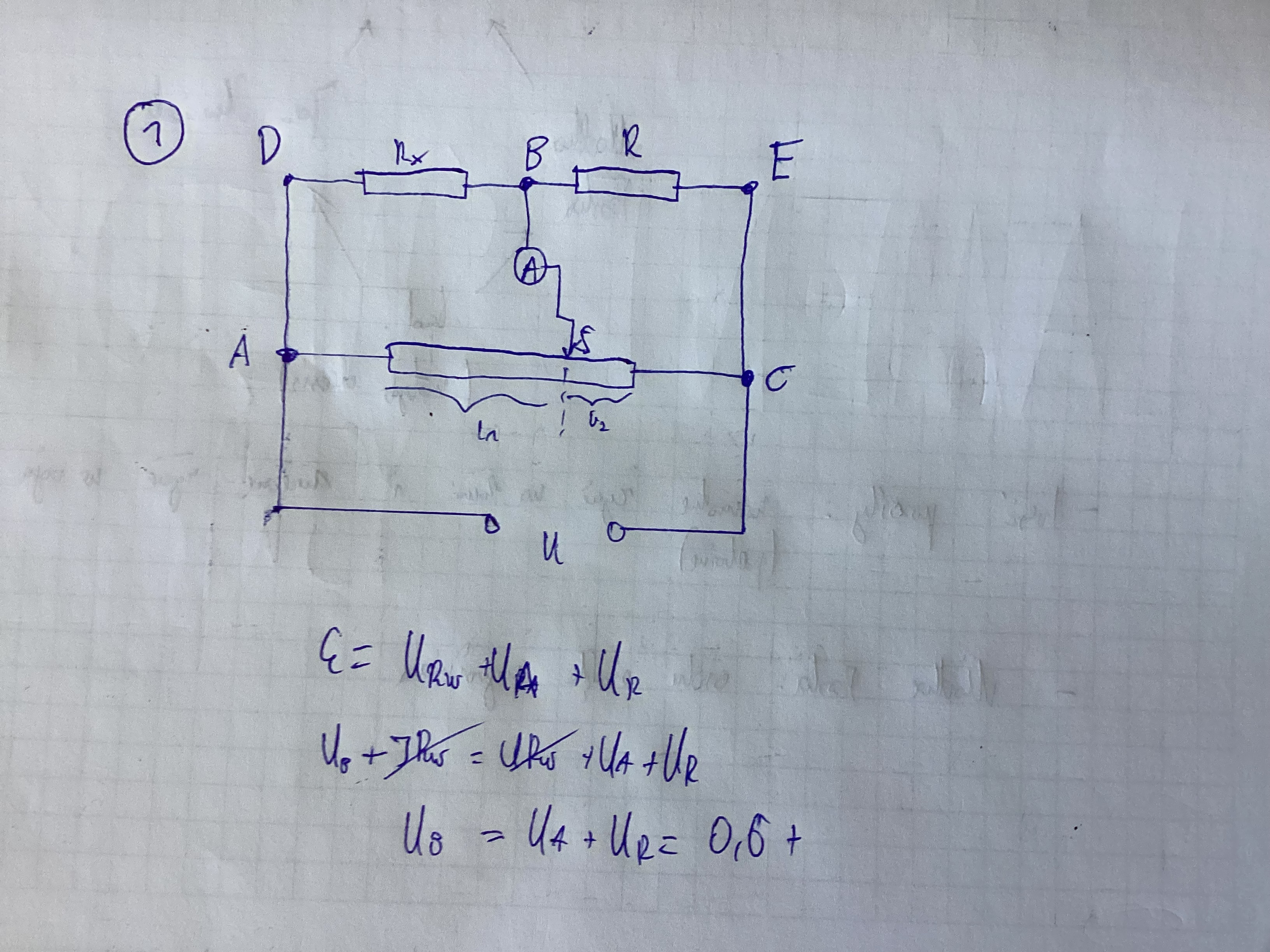 
no i to jest dokładnie to samo bo Udb=Uab itd. Może to jest kombinowanie, ale czy takie dodawanie sobie punktów jak tu zrobiłem w celu bardziej klarownego zrozumienia równości tych napięć jest poprawne?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
tak, jak najbardziej możesz sobie takie punkty dodać jeśli Ci to pomaga :) i faktycznie punkt A jest tym samym co punkt D, a punkt C jest tym samym co punkt E. I to pisałem wcześniej dotyczy dokładnie takiej właśnie rzeczy - mianowicie właśnie z uwagi na fakt, że między B i S prąd nie płynie, to punkty B i S możemy traktować jako ten sam punkt (tak jak A i D, tak jak C i E).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak jest - Twój rysunek to równoważna postać tego obwodu.
18.1: Tak jest :)
18.2: Dobrze rozumujesz. A to, że Uab = Uas i Ubc = Usc wynika właśnie z tego, że w gałęzi BS prąd nie płynie :) Bo skoro tam prąd nie płynie, to oznacza to, że w punktach B i S mamy takie same potencjały - można zatem przyjąć, że to jest dokładnie ten sam punkt pod kątem napięcia. Czyli dostajemy faktycnzie, że Uab to inaczej Uas i Ubc to inaczej Usc.