Arkusz 3 Zad 3
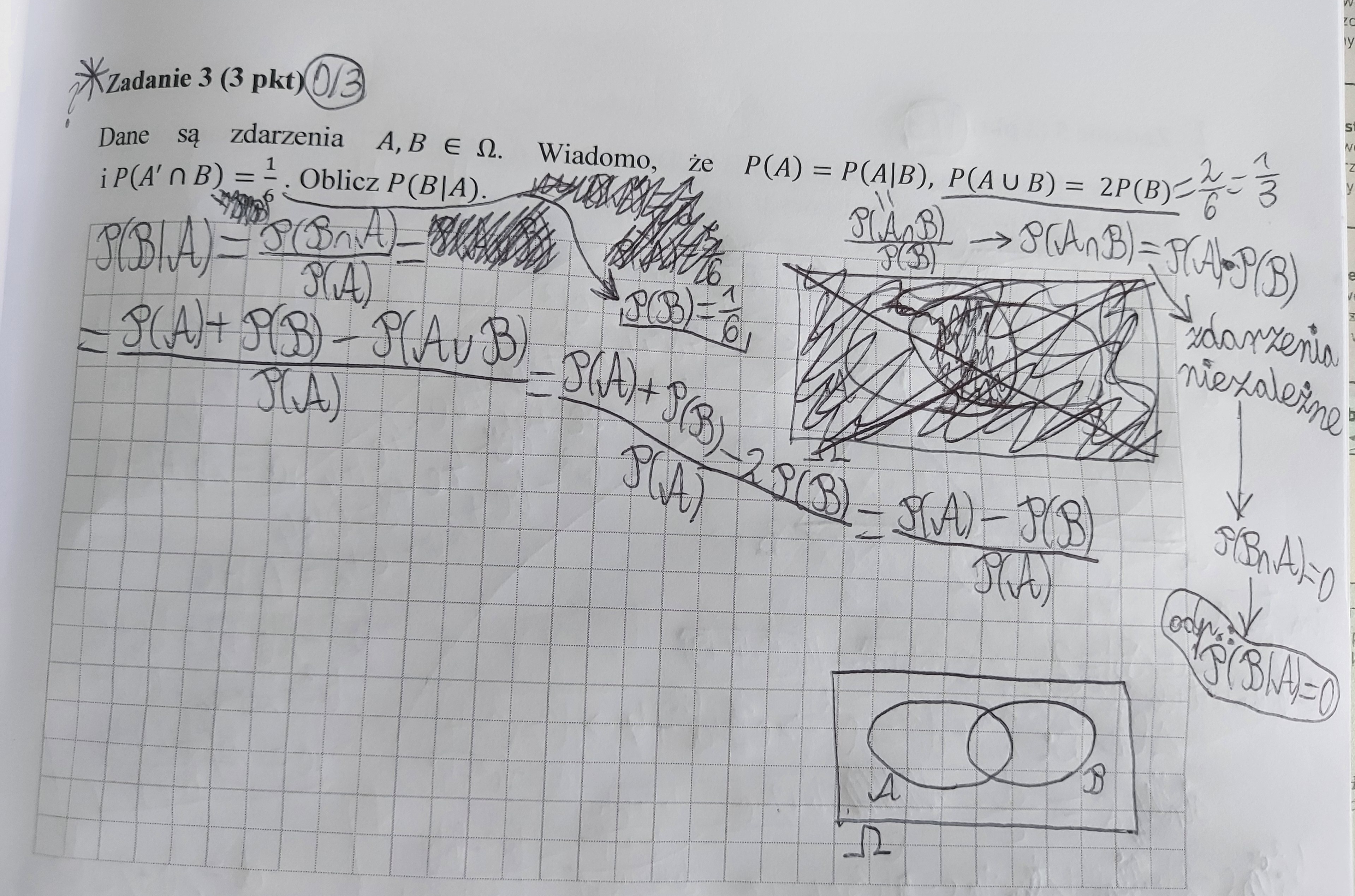
Czy nie jest tak, że jak zdarzenia są niezależne to są rozłączne, więc P(B|A)=0? Nie rozumiem jak rozwiązać to zadanie nawet na podstawie kryteriów.
Matematyka prawdopodobieństwo Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
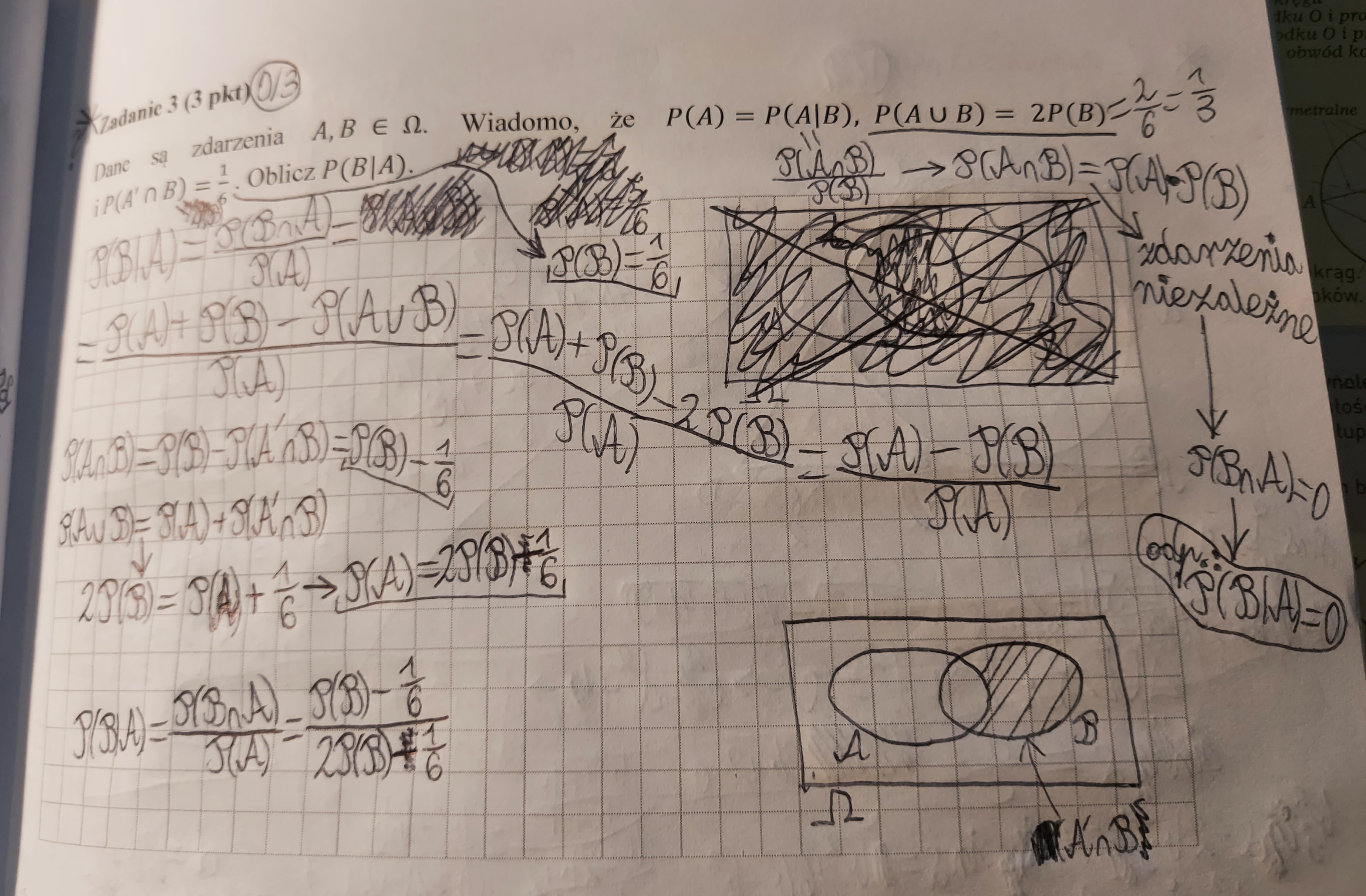
Dlaczego P(B|A)=P(B)? Wychodzi mi to co powyżej i dalej nie wiem co zrobić.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
P(B|A) = P(B) bo to zdarzenia niezależne (wykazałeś to już wcześniej), jeśli nie popełniłeś nigdzie błędu to teraz mnożąc przez mianownik dostaniesz równanie kwadratowe ze zmienną P(B).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przecież przeprowadziłeś bardzo podobny dowód na samej górze, gdzie wykazałeś niezależność tych zdarzeń.
Popatrz: P(B|A) = P(AnB)/P(A) = P(A)*P(B)/P(A) = P(B)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Faktycznie, ale teraz na podstawie odpowiedzi widzę, że mam błąd we wzorze funkcji kwadratowej 2P²-7/6P+1/6=0 i przy P² współczynnik powinien być a=1 i nie wiem gdzie jest błąd, bo w treści było dane P(a u b)=2*P(b).
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Masz dobrze, w odpowiedziach jest błąd.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie zachodzi taka własność jakoby zdarzenia niezależne były rozłączne, właściwie to zachodzi własność: P(B|A) = P(B), jeśli zdarzenia są niezależne.
Jako wskazówkę powiem ci, żebyś spróbował rozbić sobie P(A u B) = P(A) + P(A' n B), gdzie u to suma zbiorów, a n to iloczyn zbiorów.