Arkusz 3 Zad 10
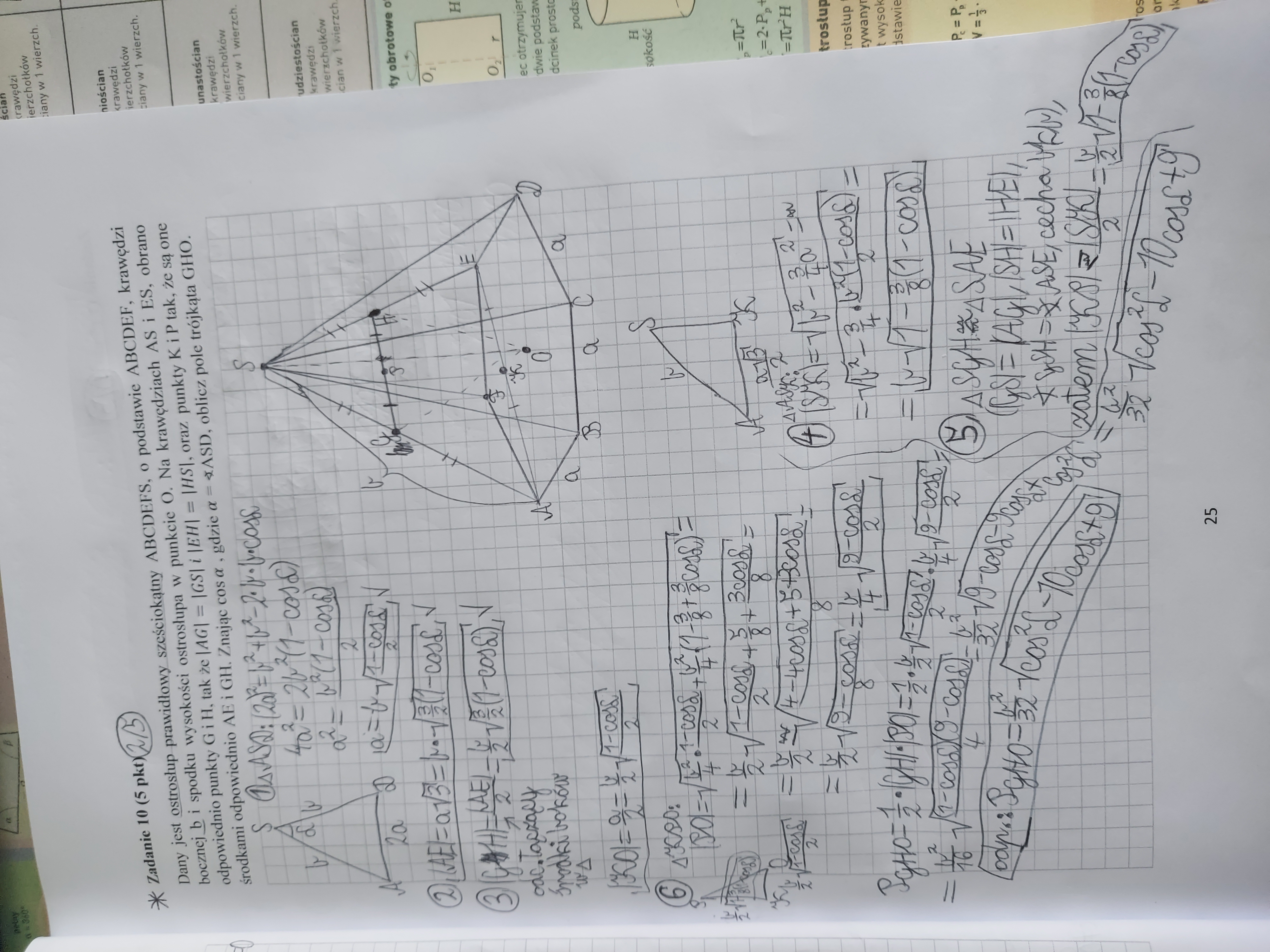
Nie rozumiem gdzie mam błąd. Do momentu obliczenia długości odcinka GH mam dobrze.
Matematyka stereometria Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli ten kąt byłby prosty gdyby odcinek AE był najdłuższą przekątną tego sześciokąta?
Jak mógłbym kontynuować to rozwiązanie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zauważ, że |OP| = |PK| = |SP|, możesz to wykazać biorąc trójkąt KOS, jest on prostokątny, a OP to środkowa i z twierdzenia dostajesz to.
Gdyby AE była główną przekątną to O=K czyli kąta w ogóle nie ma.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Widzę, że SP=PK, ale nie rozumiem z jakiego twierdzenia wynika, że OP=PK=PS. Takie coś zachodziło chyba tylko w trójkącie prostokątnym równoramiennym.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zachodzi to w każdym trójkącie prostokątnym, bo odcinek łączący wierzchołek kąta prostego z środkiem przeciwprostokątnej to promień trójkąta opisanego na tym trójkącie, a przeciwprostokątna to średnica.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
6. Trójkąt KPO nie jest prostokątny, bo kąt PKO nie jest prosty.