2020.11

11.1: 1 - Dlaczego to jest prawdą skoro elektron nie jest nukleonem?
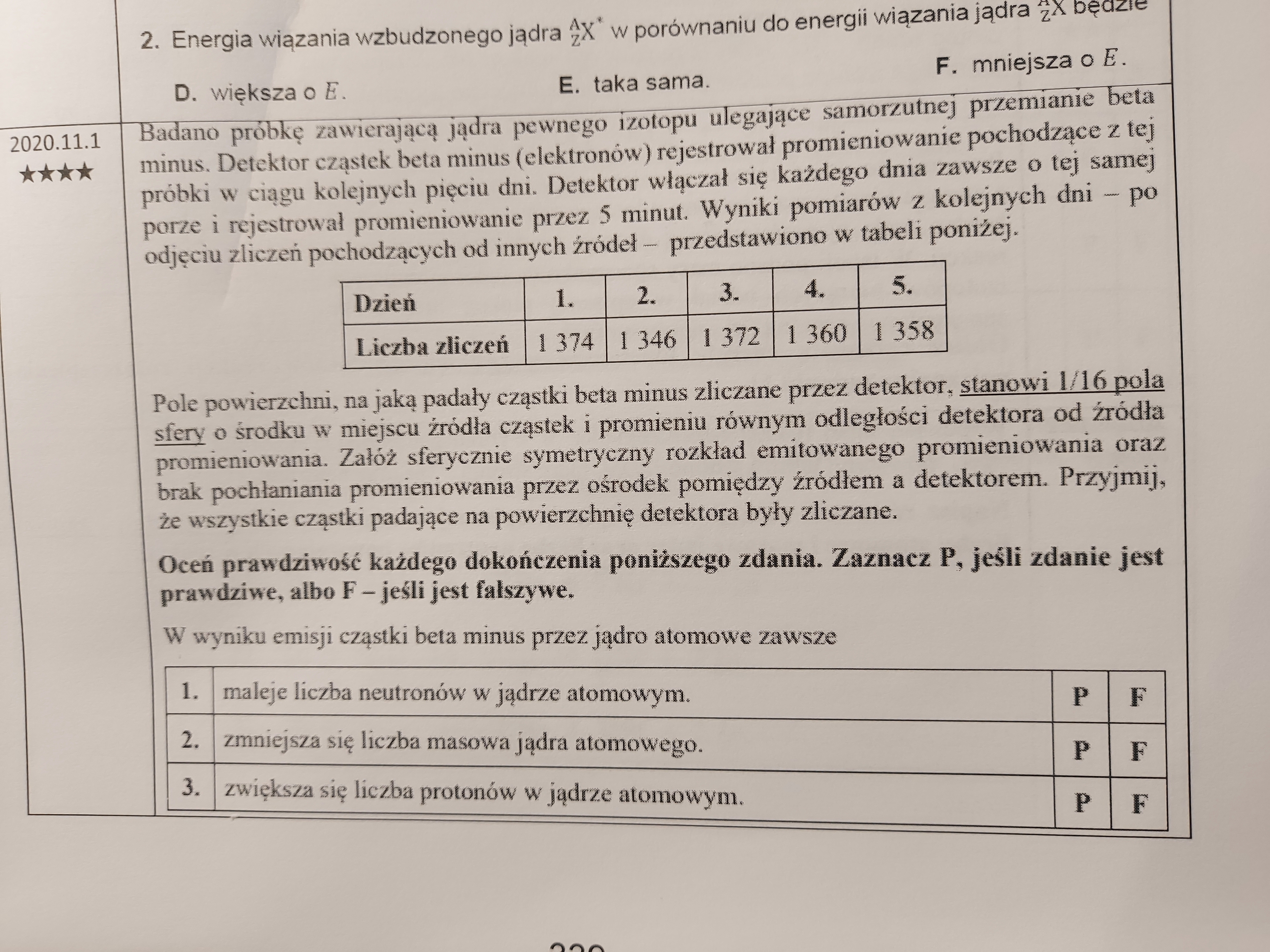
11.2: Dlaczego odpowiedź C jest poprawna? Bo ja to wybrałem tak na logikę ale w sumie nie rozumiem przyczyny, bo ta liczba zliczeń nie maleje z dnia na dzień, tylko czasem rośnie a czasem maleje.
11.3: Nie rozumiem dlaczego w tym zadaniu S~liczby zliczeń. Ja myślałem, że może r~liczby zliczeń i mi wyszło 4 razy mniej niż odpowiedź ale tak czy siak nie rozumiem powiązania pola powierzchni z liczbą zliczeń cząstek beta-.
Fizyka jądrowa Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
11.3: No ale równie dobrze ilość zliczonych elektronów mogłaby być wprost proporcjonalna do promienia fali jeśli mamy to traktować analogicznie do punktowego źródła dźwięku. Albo ta ilość mogłaby nawet być wprost proporcjonalna do objętości tej sfery. Dlaczego zatem takie proporcje nie zachodzą?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
11.3: Ale w przypadku np. fali dźwiękowej nie ma przecież takich zależności. Natężenie fali jest odwrotnie proporcjonalne do kwadratu odległości od źródła (I ~ 1/r^2). Nie wiem więc dlaczego miałyby takie zalezności zachodzić ;) Co więcej tutaj nie mamy tak naprawdę proporcjonalności liczby zliczeń do powierzchni sfery, chodzi natomiast właśnie o to co napisałem powyżej, tzn. ponieważ detektor stanowi tylko 1/16 powierzchni całej sfery, to wyłapuje on tylko 1/16 wszystkich cząstek. Stąd to mnożenie razy 16.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli powinniśmy wiedzieć, że ta ilość zliczanych cząstek jest proporcjonalna do natężenia dźwięku?
A to z wyłapywaniem 1/16 cząstek czyli pośrednio zależność od pola oznaczałoby, że cząstki te poruszają się w dwóch wymiarach? Co z trzecim wymiarem w takim razie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tzn. żeby nie było - tu nie ma żadnego natężenia dźwięku, ja tylko poczyniłem taką analogię, żeby to sobie łatwiej wyobrazić. Więc nie ma tu żadnego związku między liczbą zliczanych cząstek a natężeniem żadnego dźwięku.
W trzech wymiarach - jeśli coś rozchodzi się z jednego punktu we wszystkie strony, to rozchodzi się to w powierzchnię kuli, która jest sferą. Więc już tutaj uwzględnione są trzy wymiary (sfera jest przecież trójwymiarową powierzchnią).
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To nie do końca dalej rozumiem dlaczego patrzymy na pole a nie na objętość?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Hmm, ale nie bardzo szczerze mówiąc rozumiem w jaki sposób chciałbyś tutaj brać pod uwagę objętość? Sytuacja wygląda tak, że emitowane cząstki lecą we wszystkie strony, więc "rozchodzą" się w sferę, w środku której znajduje się źródło promieniowania. I teraz 1/16 powierzchni tej sfery zajmuje powierzchnia detektora (poniżej na rysunku np. to co na czerwono). Żeby wyłapać wszystkie cząstki, trzeba by pokryć detektorami całą sferę, czyli 16 razy większą powierzchnię. To oznacza, że wszystkich cząstek jest 16 razy więcej niż to co łapie pojedynczy detektor.
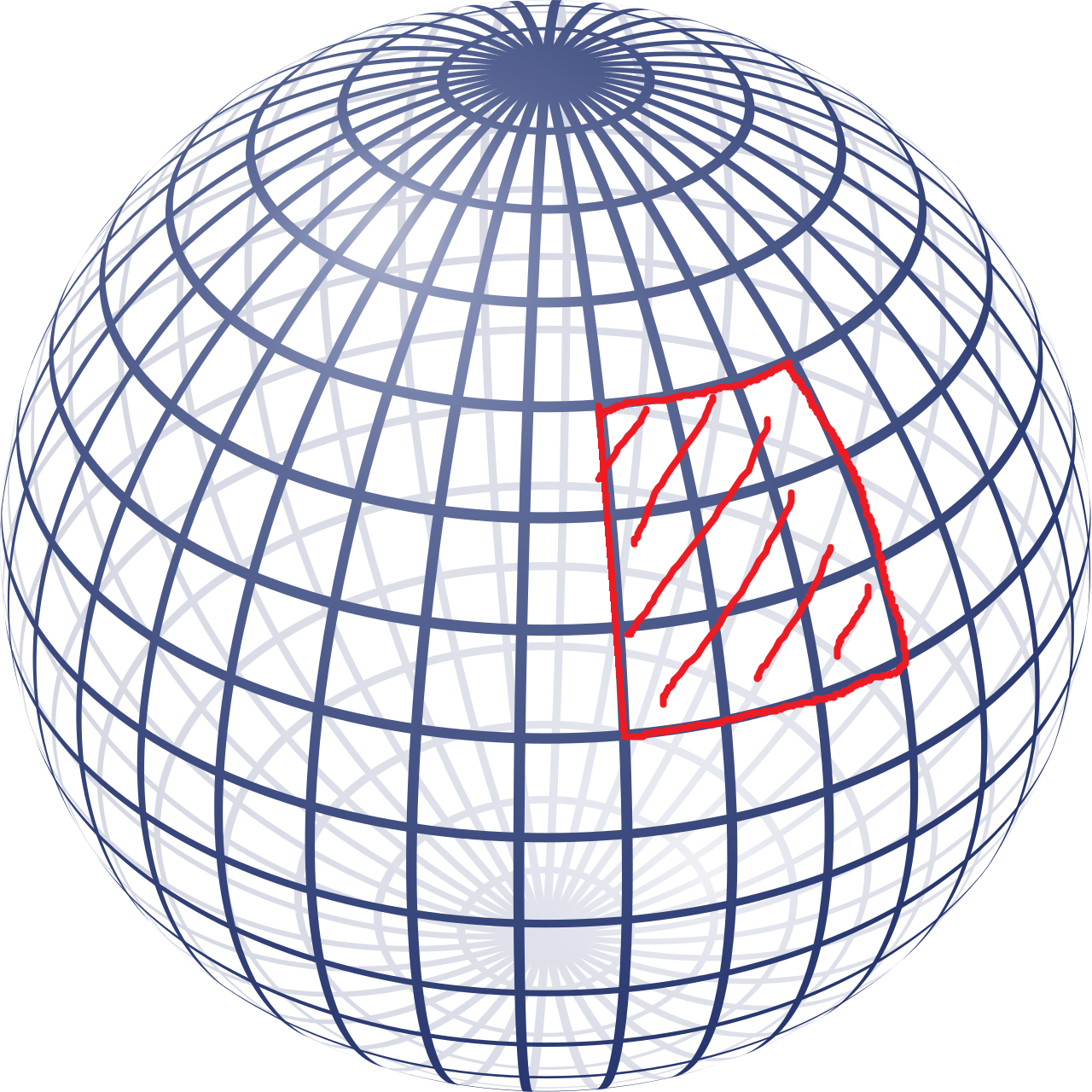
Jeśli masz jakąś swoją propozycję z tą objętością to ją przedstaw, bo ja nie widzę sposobu jak tu zaprząc w to wszystko objętość kuli ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chyba zaczynam to rozumieć. Czyli może objętość tutaj nie ma sensu, bo detektor ma kształt dwuwymiarowy?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No w sumie tak, tzn. ważne jest, że jego powierzchnia rejestrująca cząstki jest własnie powierzchnią, czyli czymś co ma pole, a nie objętość.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
11.1: No ale, żeby wyemitowany został elektron, to najpierw neutron musi w jądrze ulec przemianie w proton (zapisywaliśmy to na samym początku zajęć nr 26). Więc jest to prawda.
11.2: No właśnie - a wiemy przecież, że charakter rozpadów jest przypadkowy. Skoro zatem nie zauważamy wyraźnego spadku liczby zliczeń, tylko ona sobie ciągle oscyluje wokół jakiejś w przybliżeniu ustalonej wartości (raz troszkę więcej, raz troszkę mniej), to znaczy, że można w pewnym przybliżeniu stwierdzić, że ta liczba zliczeń w ogóle się nie zmienia z dnia na dzień. A to oznacza, że każdego dnia mamy w przybliżeniu tyle samo jąder emitujących rejestrowane elektrony. A to oznacza, że te jądra rozpadają się bardzo "powoli" - czyli każdego dnia ubywa tak niewielka część tych jąder, że nie jest to zauważalne. A to oznacza, że czas połowicznego rozpadu tego izotopu musi być znacznie dłuższy niż kilka dni.
11.3: Trzeba wyobrazić sobie, że mamy naszą próbkę i ona emituje te elektrony we wszystkie strony jednakowo (żaden kierunek nie jest wyróżniony) - coś jak punktowe źródło fali, np. dźwiękowej. Czyli gdybyśmy teraz mogli to źródło "obłożyć" ze wszystkich stron detektorami (zamknąć to źródło w takiej sferze z detektorów), to bylibyśmy w stanie wyłapać wszystkie emitowane elektrony. Ale my mamy tylko jeden detektor, którego powierzchnia stanowi 1/16 powierzchni takiej sfery, stąd wyłapujemy tylko 1/16 wszystkich elektronów. Więc jeśli pomnożymy rejestrowaną liczbę elektronów razy 16 to dostaniemy ile wszystkich elektronów zostało wyemitowanych.