Arkusz 4 Zad 6
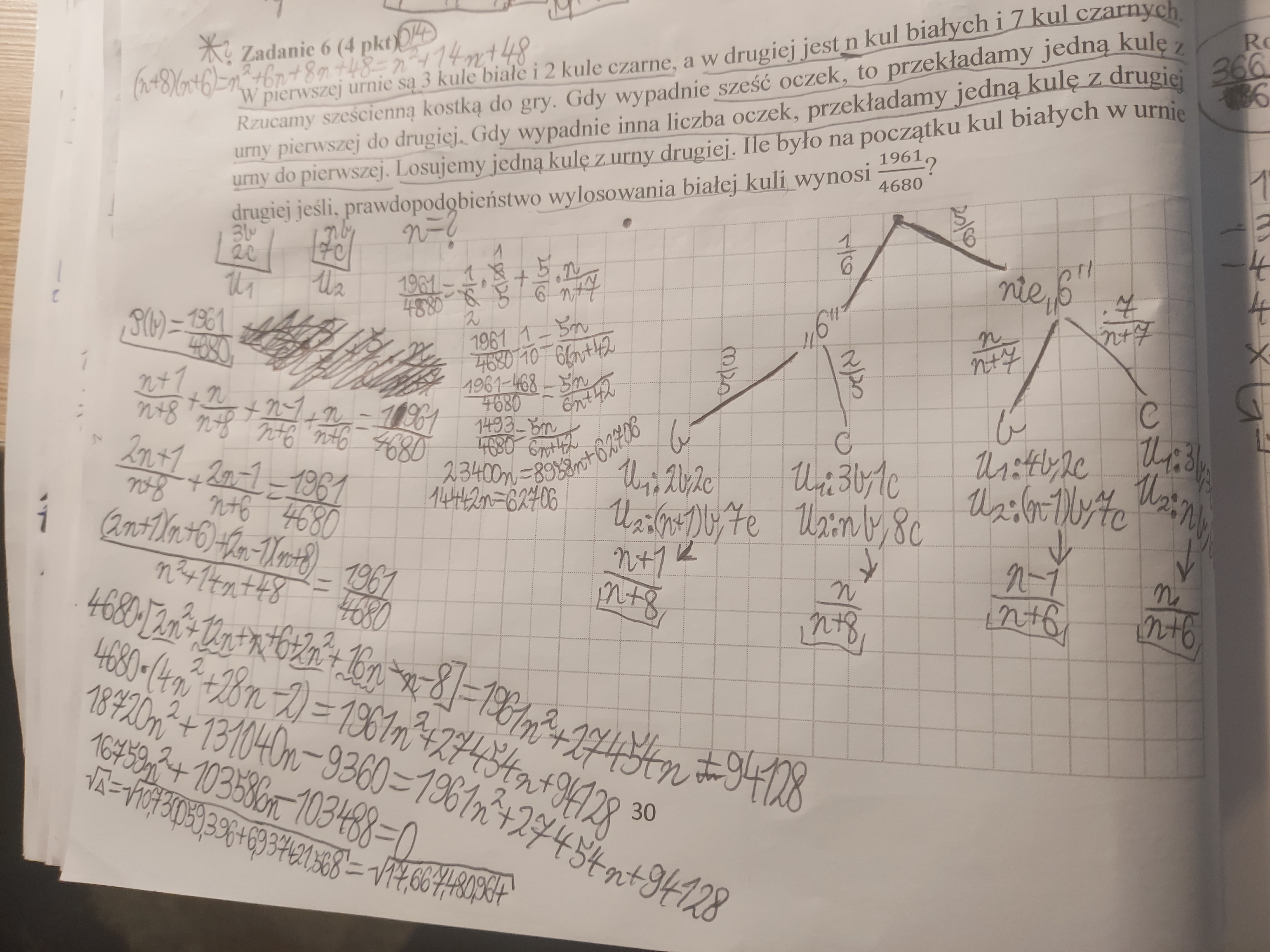
Nie rozumiem dlaczego w tym konkretnym zadaniu trzeba przemnażać prawdopodobieństwa z kolejnych gałęzi drzewka a nie można po prostu dodać ostatnich "etapów" drzewka w ten sposób jak zrobiłem to w lewej części zdjęcia.
Matematyka prawdopodobieństwo Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Faktycznie. A gdzie w obliczeniach teraz mam błąd? Bo liczby wychodzą mi bardzo duże.
Obliczenia pod kreską i na brązowej kartce.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przeanalizuj każde obliczenia po kolei skrupulatnie - ewentualnie z użyciem kalkulatora. Szukanie swoich własnych błędów jest również rozwojowe.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przeanalizowałem to już z 3 razy, ale dalej nie mogę znaleźć błędu. Widzę natomiast, że jest on gdzieś w obliczeniach, bo delta jaka mi wychodzi to liczba niecałkowita.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Masz błąd na żółtej kartce, zauważ, że 1680 z pierwszego mianownika i 4680 wyglądają dosyć podobnie, oraz 21 i 1961 również, nasuwa się sugestia czy licznik nie będzie równy po 1961, a mianownik 4680, nie trudno wyliczyć, że jeśli n=5 to tak właśnie się dzieje, z tego wniosek płynie, że 5 to jeden z pierwiastków, stosując schemat hornera, możesz wyliczyć drugi. Nie ma sensu liczyć tak dużych delt.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A skąd liczba 1967? Poza tym wiem, że moje obliczenia są żmudne i długie, ale wydaje mi się, że powinny doprowadzić do poprawnego wyniku mimo wszystko.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Poprawiłem już komentarz masz racje, błąd powinno być 1961.
Tak twoje obliczenia powinny doprowadzić do końca, ale są żmudne i długie, na maturze nie chodzi tylko o to by otrzymać dobry wynik, ale też żeby się nie namęczyć i szybko zrobić zadanie. Deltę policzyć umie każdy, spróbuj metodą którą ci podałem (tzn przyrównać mianownik i licznik, a następnie gdy już wyliczysz, że 5 to pierwiastek to schematem hornera wyliczyć drugi pierwiastek i ewentualnie go skreślić jeśli nie będzie liczbą naturalną), ona jest bardziej rozwijająca niż kolejny raz liczenie delty z kalkulatorem.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Twój pierwszy przypadek (tzn wypadła 6 i przeniesiona została biała kula) to on zakłada, że oprócz wylosowania na końcu kuli białej na końcu wcześniej wypadła 6 i przeniesiono kule białą, więc należy to uwzględnić mnożąc po kolei 1/6 * 3/5 * (n+1)/(n+8), analogicznie pozostałe przypadki.
Gdy już policzysz wszystkie przypadki to zauważ, że ostateczne prawdopodobieństwo to suma tych prawdopodobieństw.
MUSISZ więc przemnożyć każdy z nich przez te wartości z etapów wcześniejszych.