Zad.2 cz.1|24
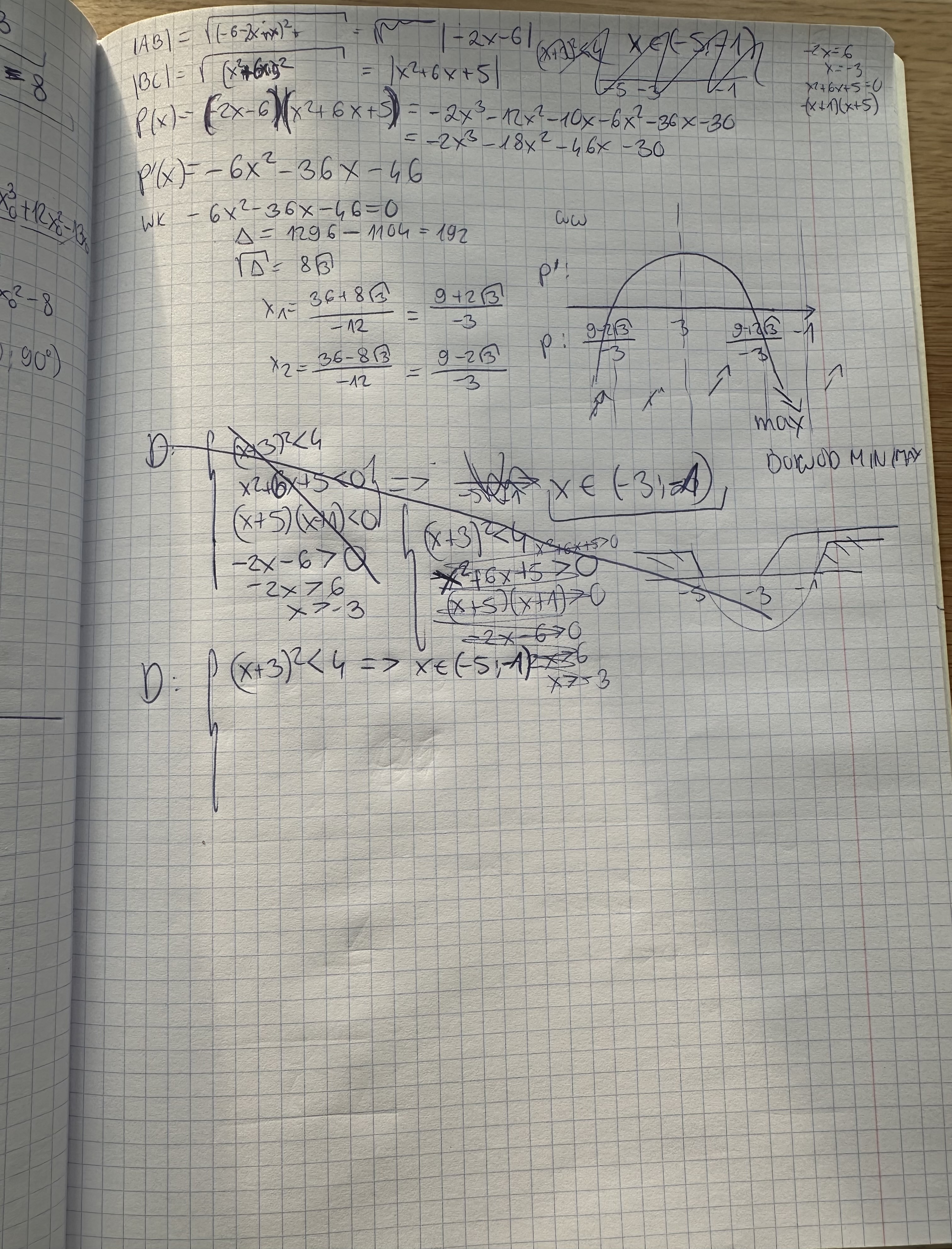
Nie rozumiem w jaki sposób opuścić wartości bezwzględne i stworzyć z nimi założenia. Czy nie należałoby postąpić -2x-6>0 i x^2+6x+5>0 ( ponieważ odcinki są >0) i (x+3)^2<4?
Zad.2 cz.1 24 Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@jarosinski ale x mozna brac z przedzialu (-5;-1) bez -3 (bo wtedy prost. n. istnieje).
Jak wstanie -4 to tak samo utworzą mi się wierzchołki. Jak mam uzasadnić Pańską dziedzinę na maturze? Nie rozumiem za bardzo co tu się z nią dzieje. Bo ok., a>0 i b>0. Co dalej?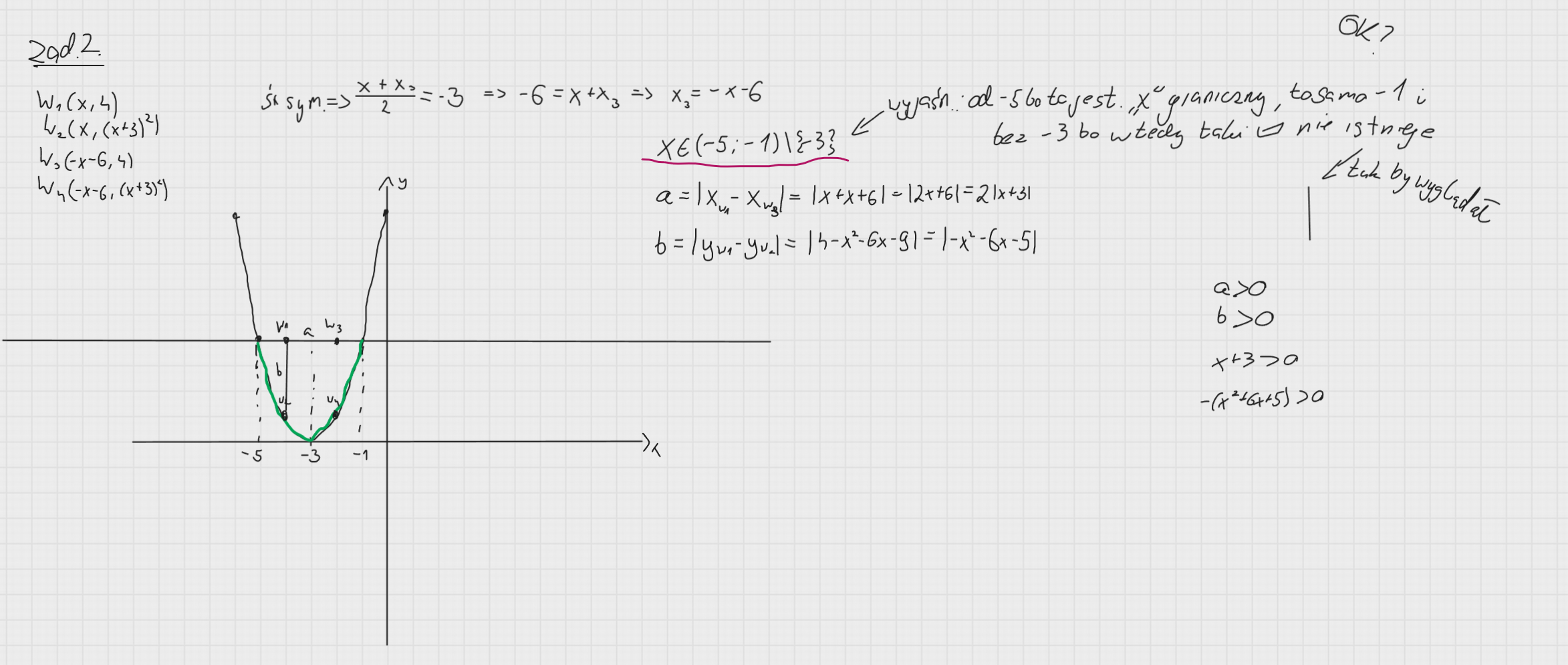
przecież dla x=-4 tak samo mamy poprawne wierchołki
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak możesz brać x z większego przedziału, ale zauważ, że jeśli weźmiesz x = -4 to będzie takie samo pole jak x = -2, bo to będą takie same prostokąty, więc po co rozpatrywać ten sam przypadek kilka razy?
Moje rozwiązanie dodatkowo eliminuje wartości bezwzględne które mogą być przeszkadzajką.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zauważ, że możesz wziąć x z przedziału (-3, -1) jako pierwszą współrzędną prawego dolnego wierzchołka, wtedy 4 - (x+3)^2 > 0 (jest to wysokość prostokąta) i 2*( x - (-3) ) > (jest to szerokość prostokąta. Eliminuje to problem wartości bezwzględnych.