Arkusz 5 Zad 4

W liczeniu wartości pomiędzy -2 a 2 masz błąd w mianowniku.

Dodatkowo piszemy lim x->-2 f(x),  a nie lim x->-2 f(-2).

Ps: nie ma sensu tu liczyć granic, wystarczy skorzystać z własności funkcji homograficznej, jeśli ich nie pamiętasz to dopiero granice.

Ale nie wiem zbytnio jak tutaj można zapisać funkcję homograficzną dla -2<x<2.

Sprowadź tą funkcję to postaci:

4/(x+2) - 3,

następnie zauważ, że, jest to funkcja 4/x przesunięta o wektor [-2, -3] i teraz będzie ci łatwiej narysować, rysunek nie musi być dokładny, najważniejsze, żebyś znał mniej więcej kształt i końcowe punkty, lub asymptoty.

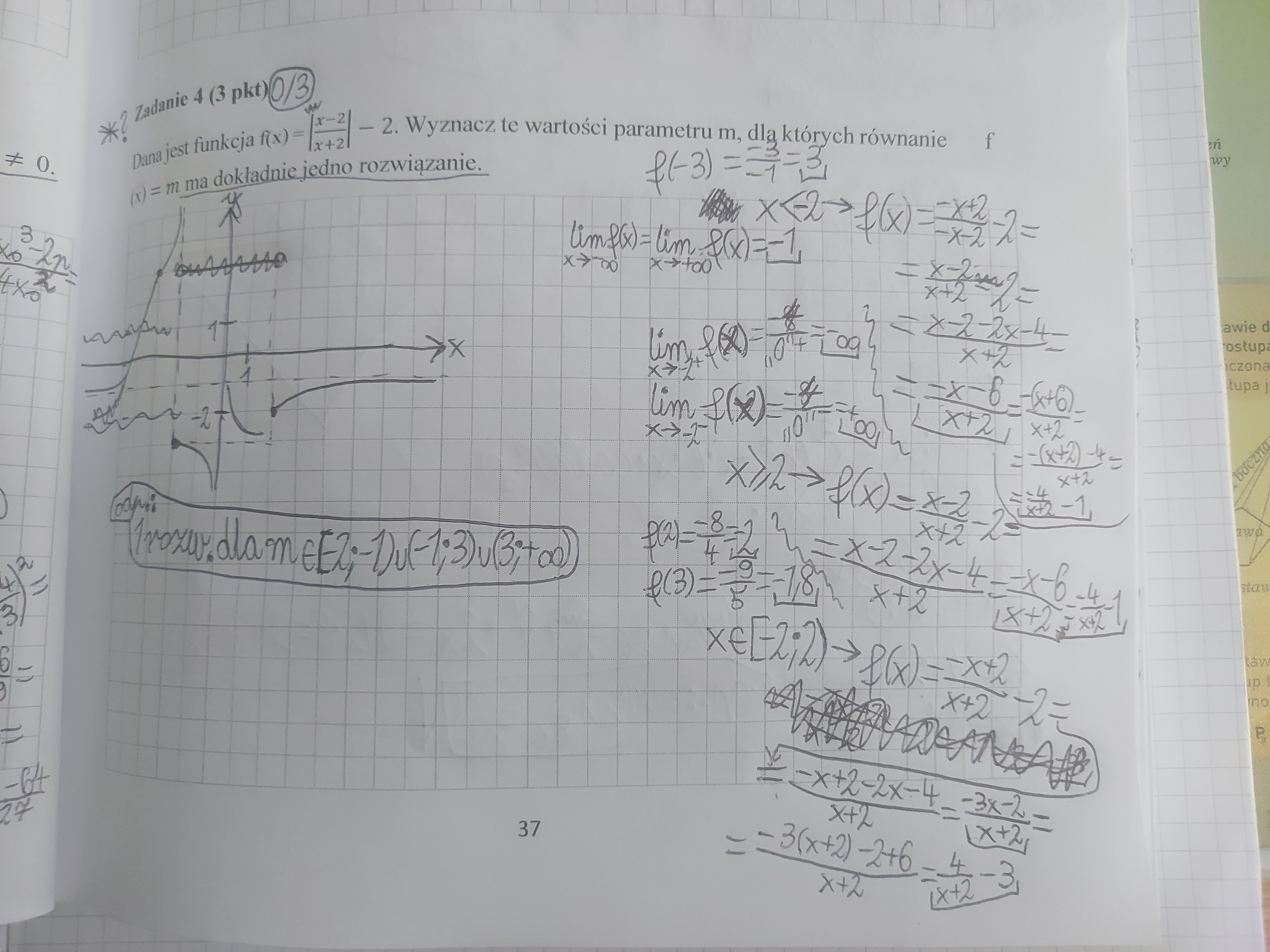
To teraz wykres wygląda tak i odpowiedź mi wychodzi (-nieskończoność;-2)u(1;+nieskończoność).

Źle przesunąłeś o wektor, trzeba też przesunąć w lewo.

Po za tym nawet jeśli założymy, że dobrze przesunąłeś to i tak jest źle, zauważ, iż ten wykres który miałeś przesunąć rozciąga się do samego dołu i góry, stad wartości powyżej 1 też mają 2 rozwiązania.

Z tęgi co rozumiem teraz wychodzi mi takie coś: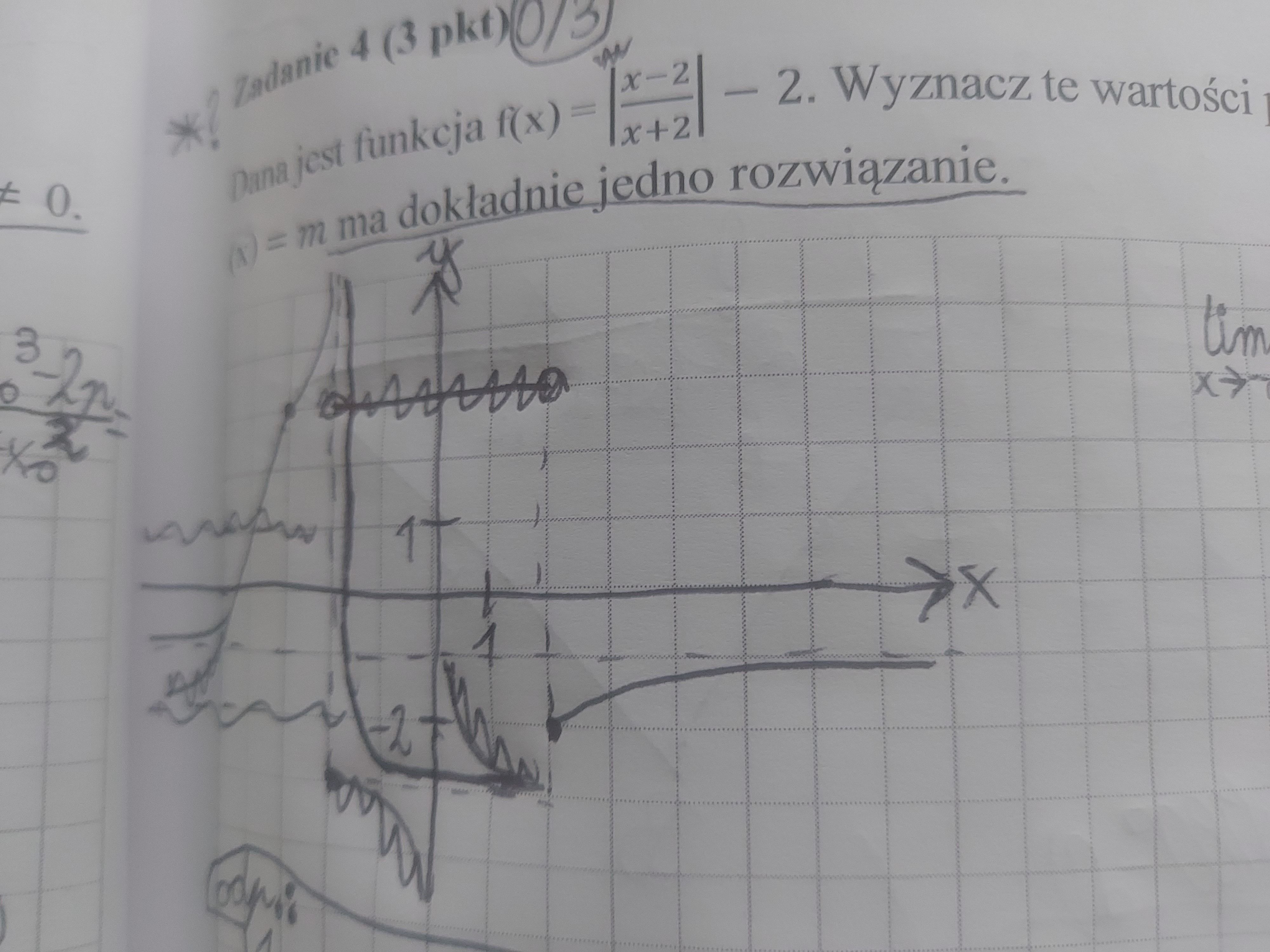

To także jest błędne.

Źle narysowałeś wykres, środkowa hiperbola powinna łączyć się z punktem rozpoczynającym prawy wykres.

Wtedy zauważ, że jedyne wartości dla których będzie tylko jedno rozwiazanie to -2 i -1.