Arkusz 7 zadanie 10
Zadanie 10 (5 pkt)
Podstawa ostrostupa jest prostokat, którego dlugosci boków sa w stosunku 3 : 1. Dwie sasiednie sciany tego ostrostupa sa prostopadte do plaszezyzny podstawy. Najdtuzsza krawedz boczna
tworzy z plaszoryzna podstawy kat a taki, ze tg a = pierwiastek z 30 / 10
-. Oblicz miary katów jakie tworza dwie
pozostate sciany ostrostupa z plaszczyzna podstawy.
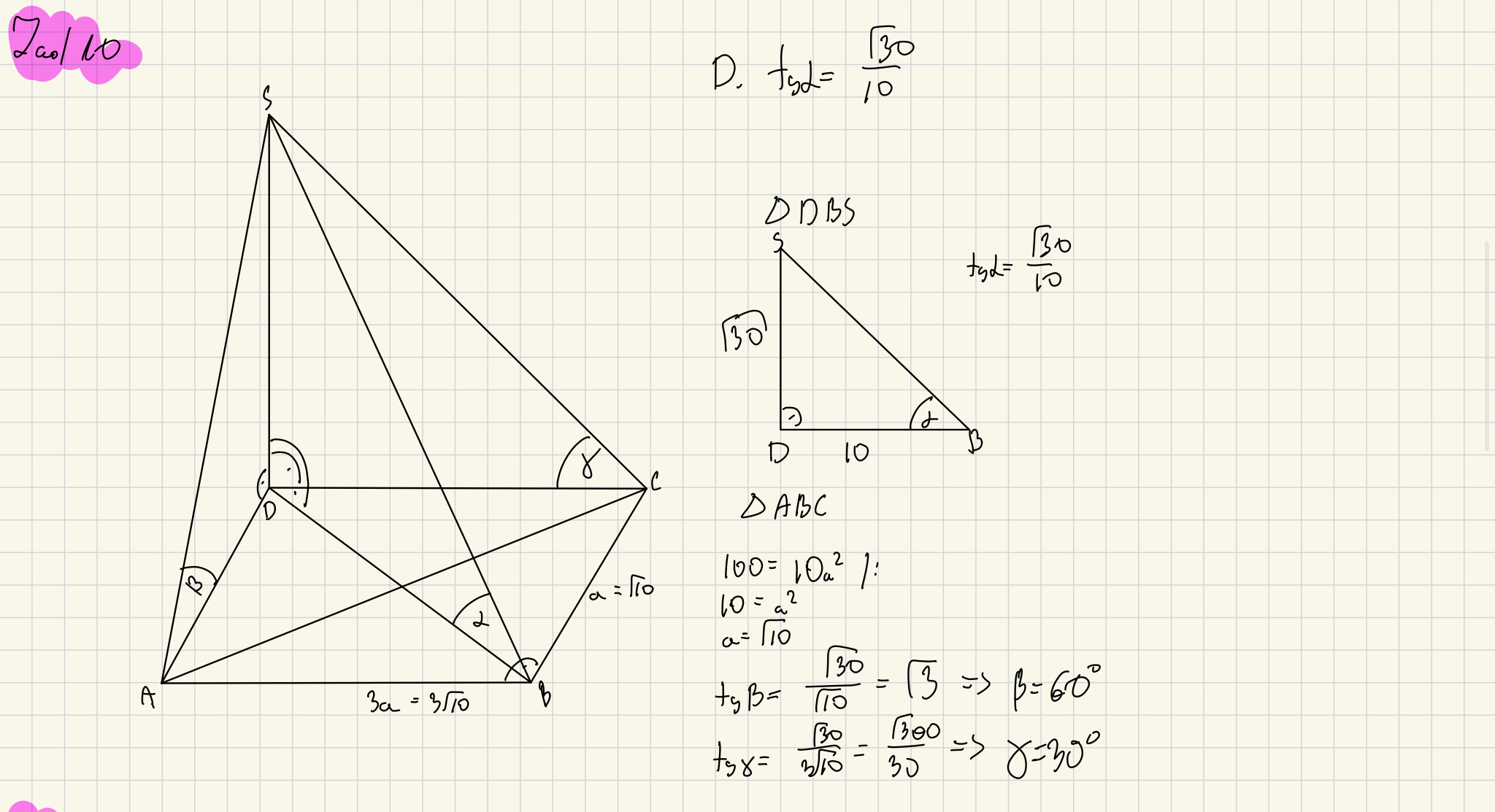Czy tak zrobione to zadanie jest poprawny? W odpowiedziach kąty b i g wyszły takie same ale jest tam punkt za policzenie odcinka BS oraz jest tam wyrażona literka a jako nie wiadoma. A nie rozumiem czemu skoro wiedząc że tga równy jest pierwiastek z 30/10 i trójkąt jest prost możemy obliczyć DB a potem z Pitagorasa i wyznaczyć długość a .
Matematyka stereometria Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czyli jak rozumiem jakbym zaznaczył boki z tg jako pierw z 30 a oraz 10a to po zrobieniu wszystkiego identycznie wyszło by mi to samo? Bo w tedy a jako zmienne sie skrocą przy funkcji trygonometrycznej.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
bo funkcje trygonometryczne wyrażają stosunek wielkości. Równie dobrze a mogło by się równać n sqrt10, inne wartości też n krotnie większe a stosunek wyszedłby taki sam.