Arkusz 7 zadanie 12 dziedzina funkcji
Zadanie 12 (7 pkt)
Wiasciciel parku w ksztaicie trojkata prostokatnego o kacie ostrym 30° i krotszej przyprostokatnej o dtugosci 40m zamierza postawic prostokatne lodowisko o bokach x, y. Jeden z boków lodowiska zawiera sie w przeciwprostokatnej.
a) wykaz, ze pole lodowska mozna wyrazié wzorem: f (y) = V3(80y-y^2)/4
+
b) podaj dziedzine funkeji f.
c)
oblicz maksymalne pole lodowiska i podaj jego wymiary.
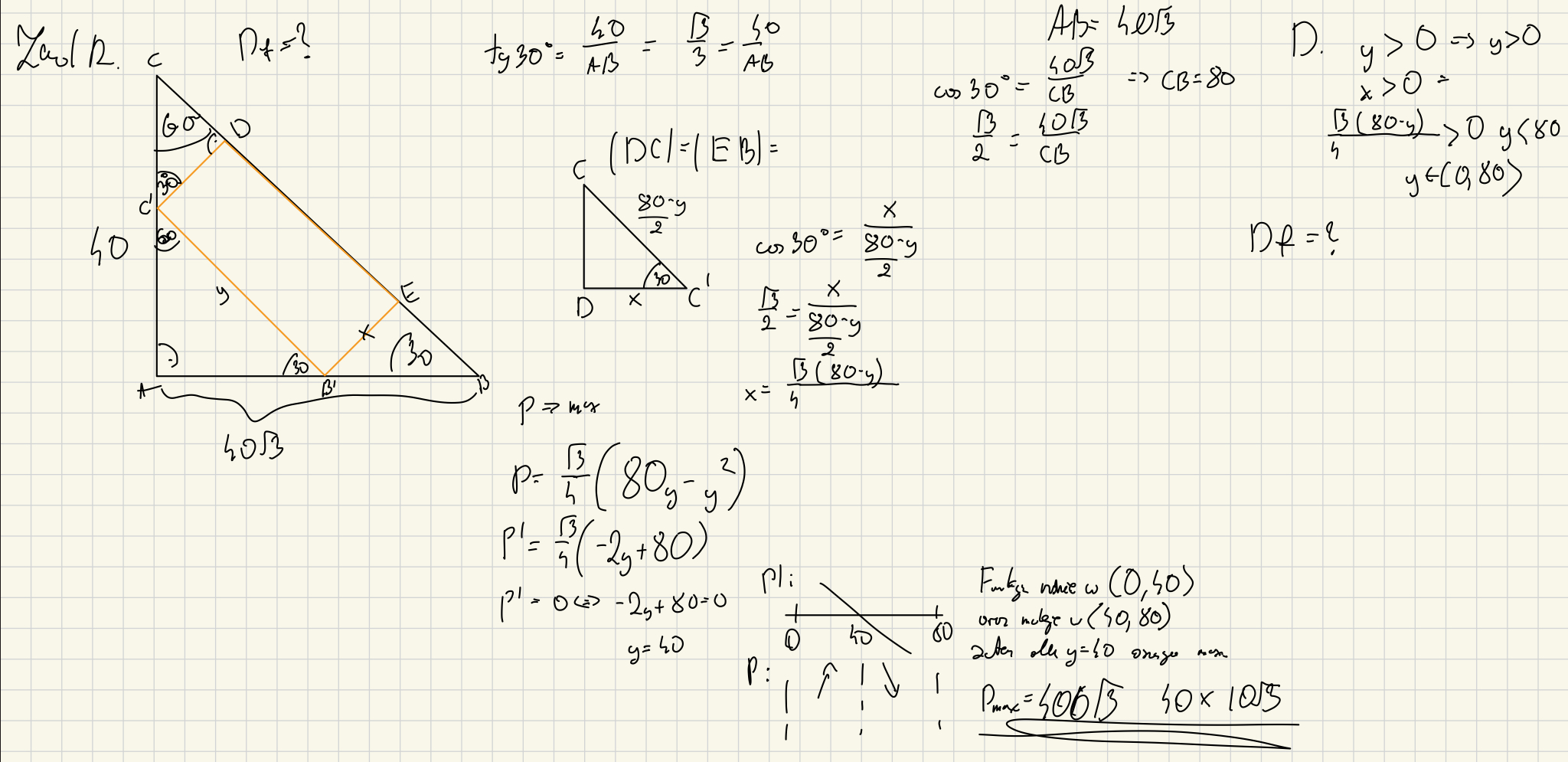Nie wiem jak wyznaczyć dziedzinę funkcji początkowo dawałem że pole ze zmienną y musi być większe od 0 ale mi nie wychodzi taka jaka ma być czyli (0,20V3). Gdzie robię błąd proszę o pomoc.
Matematyka optymalizacja Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Musisz uwzględnić to, że x musi być mniejszy niż wysokość trójkąta ABC opuszczona na bok BC, wtedy wyjdzie ci prawidłowa dziedzina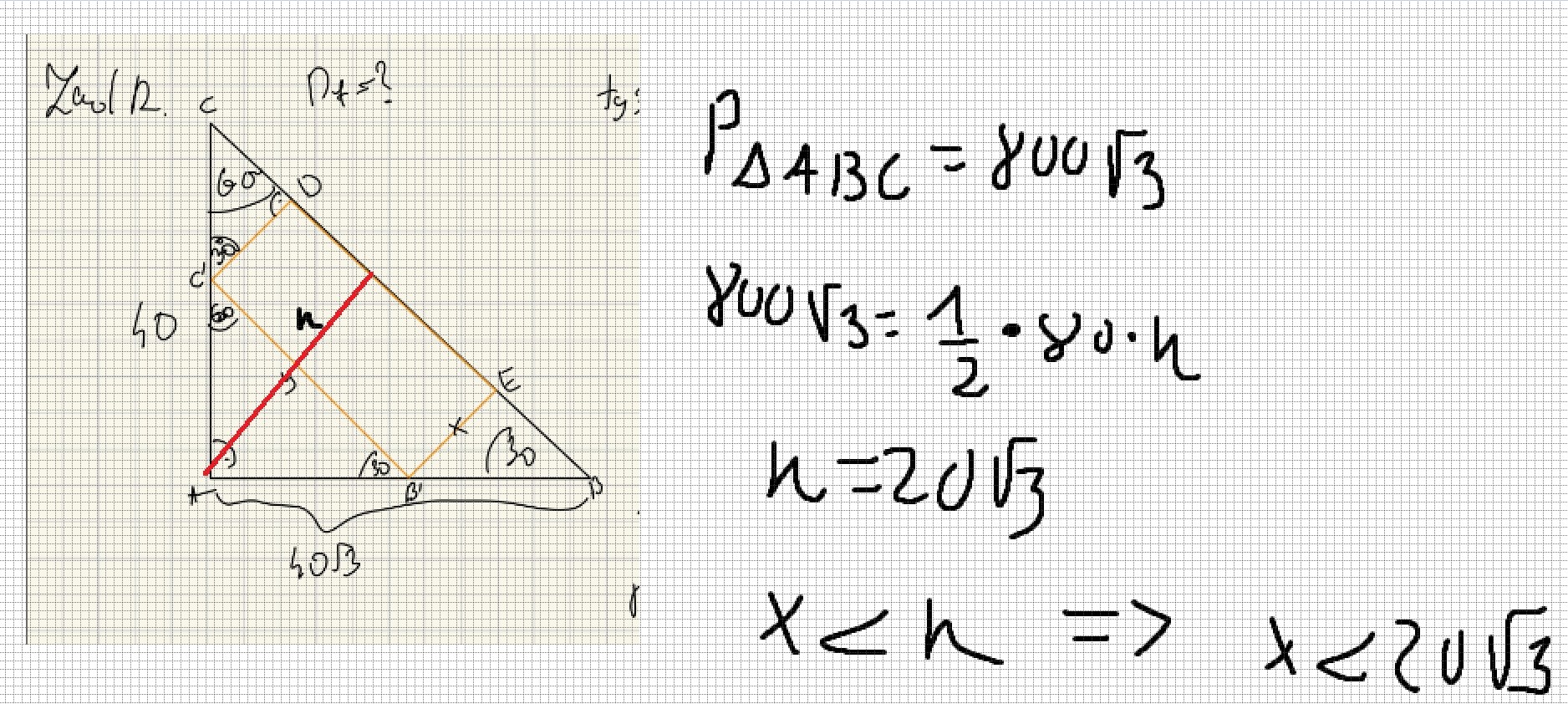 
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dla mnie dalej jest jedna rzecz niejasna.
To jest dziedzina x - x należy (0; 20pierw_z_3) i to jest jasne.
Natomiast my mamy wyznaczyć dziedzinę funkcji od y. Ta dziedzina to (0;80). I wartości y i x są powiązane ze sobą - jak y dąży do 0 do x dąży do 20_pierw_z_3, jak y dąży do 80 to x dąży do zera.
Dziedzina w kluczu jednak dotyczy funkcji x, czy poprawna dziedzina to nie (0;80) bo mamy funkcję y?
Gwiazdkami oznaczam dziedziny poszczególnych boków i funkcji na końcu, Wynik wychodzi dobry, przy wyliczeniu pola nie musimy w ogóle wrócić do x, mamy wzór uzależniony tylko od y.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Marcin
To zależy od tego który bok jak oznaczysz.
Twoje rozwiązanie jest również ok.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To ja też poczekam na odpowiedź