maja 83 wyśw. 04-04-2025 19:31

arkusz 2, zad 10

Dany jest okrąg „h" o równaniu: x ^ 2 + (y + 3) ^ 2 = 4 i prosta “k": y - 2 = 0 . Wyznacz równanie krzywej zawierającej środki wszystkich okręgów, które są styczne zewnętrznie do okręgu “h” i jednocześnie styczne do prostej “k”

Czemu jak liczymy d(S, k) to r=2-y, a nie np r=y-2 skoro wychodzi r=|y-2|? Nie rozumiem dlaczego pomimo wartosci bezwzglednej jest tylko 1 rozwiazanie :/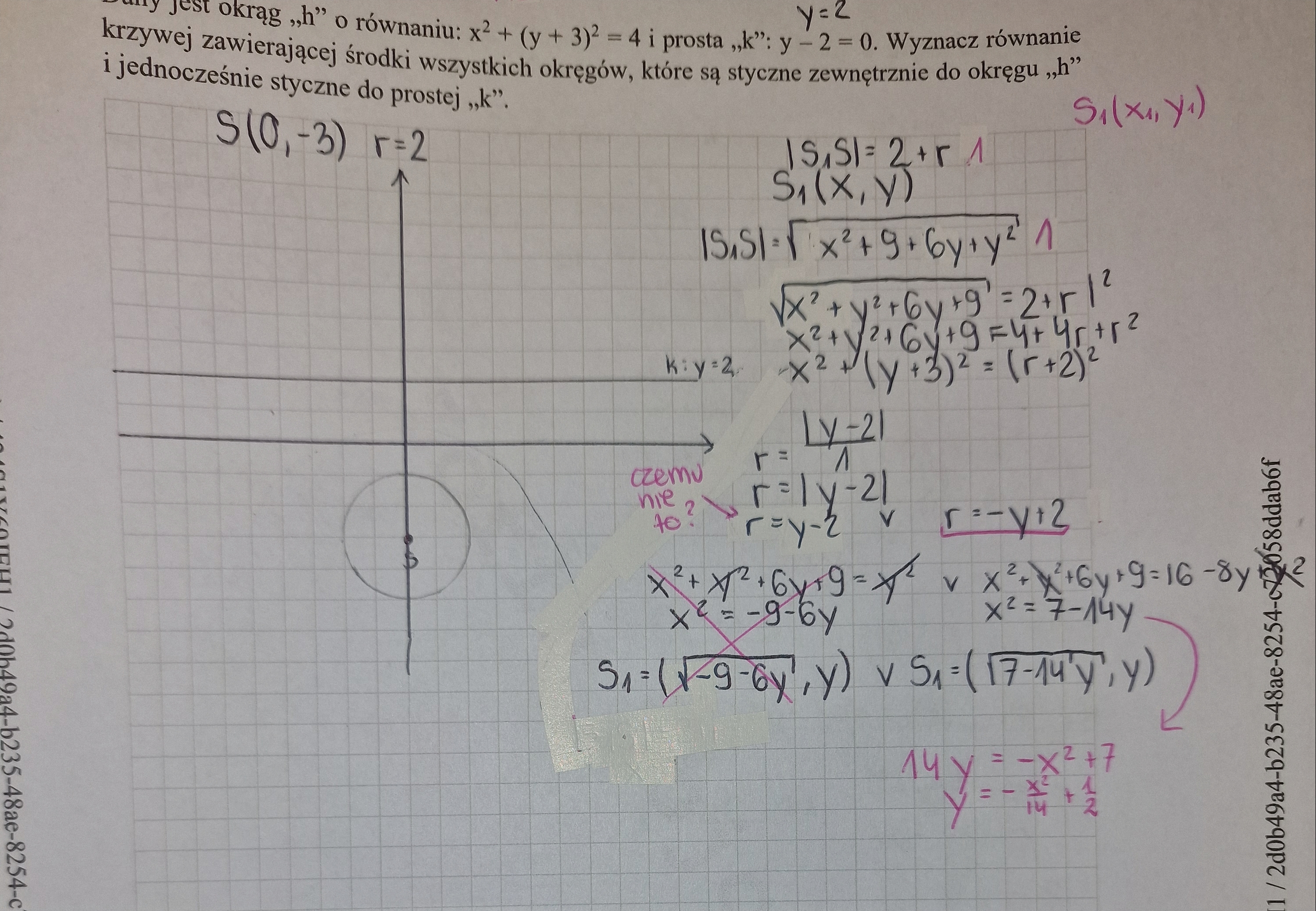

arkusze Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 06-04-2025 23:20

W uproszczeniu wynika to z faktu, że przy wyprowadzaniu równania korzysta się z dwóch możliwych sposobów spełnienia warunku, "odległość środka od prostej równa się promień". Dostajemy zatem dwa rozwiązania, ale jedno z nich okazuje się sprzeczne z geometrią zadania tzn. dla drugiego rozwiązania okazuje się niemożliwe aby krzywa z równania była rzeczywistym miejscem środków okręgów stycznych zewnętrznie dodanego okręgu h i stycznych do prostej y=2.

maja 07-04-2025 13:32

A jak sprawdzić, ze 1 wynik nie spelnia warunkow?


jarosinski 07-04-2025 21:29

Tutaj odpowiedziałem na to pytanie: https://forum.szkolamaturzystow.pl/wpis/1743068109-arkusz-2

Zadzwoń teraz Dotknij, aby się ze mną skontaktować.